题目内容
15. 在△ABC中,AB=BC,BD平分∠ABC,四边形ABED是平行四边形,DE交BC于点F,连接CE.当△ABC满足什么条件时,四边形BECD是正方形.
在△ABC中,AB=BC,BD平分∠ABC,四边形ABED是平行四边形,DE交BC于点F,连接CE.当△ABC满足什么条件时,四边形BECD是正方形.
分析 根据已知条件易推知四边形BECD是平行四边形.结合等腰△ABC“三线合一”的性质证得BD⊥AC,即∠BDC=90°,所以由“有一内角为直角的平行四边形是矩形”得到?BECD是矩形,进而得出四边形BECD是正方形.
解答 解:当△ABC满足∠ABC=90°时,四边形BECD是正方形,
理由:∵AB=BC,BD平分∠ABC,
∴BD⊥AC,AD=CD.
∵四边形ABED是平行四边形,
∴BE∥AD,BE=AD,
∴BE=CD,
∴四边形BECD是平行四边形.
∵BD⊥AC,
∴∠BDC=90°,
∴?BECD是矩形,
又∵AB=BC,∠ABC=90°,BD平分∠ABC,
∴AD=BD=DC,
∴矩形BECD是正方形.
点评 本题考查了矩形的判定以及正方形的判定,正确把握矩形的定义:有一个角是直角的平行四边形是矩形是解题关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 如图,在平面直角坐标系内有两点A(-2,0),B($\frac{1}{2}$,0),CB所在直线的方程为y=2x+b,连接AC,求证:△AOC∽△COB.
如图,在平面直角坐标系内有两点A(-2,0),B($\frac{1}{2}$,0),CB所在直线的方程为y=2x+b,连接AC,求证:△AOC∽△COB.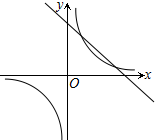 已知双曲线y=$\frac{6}{x}$和直线y=kx+4.
已知双曲线y=$\frac{6}{x}$和直线y=kx+4.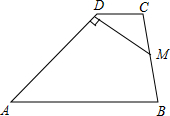 梯形ABCD中,腰AD=10厘米,梯形的面积为70平方厘米,则由腰BC的中点M到直线AD的距离为多少厘米?
梯形ABCD中,腰AD=10厘米,梯形的面积为70平方厘米,则由腰BC的中点M到直线AD的距离为多少厘米? 如图,C是路段AB的中点,两人从C同时出发,以相同的速度分别沿两条直线行走,并同时到达D,E两地,DA⊥AB,EB⊥AB,D,E与路段AB的距离相等吗?为什么?
如图,C是路段AB的中点,两人从C同时出发,以相同的速度分别沿两条直线行走,并同时到达D,E两地,DA⊥AB,EB⊥AB,D,E与路段AB的距离相等吗?为什么?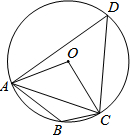 如图,四边形ABCD内接于⊙O,∠OAC=40°,求∠ABC的度数.
如图,四边形ABCD内接于⊙O,∠OAC=40°,求∠ABC的度数.