题目内容
4.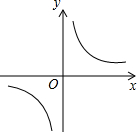 已知反比例函数y=$\frac{k-2}{x}$的图象如图,则一元二次方程x2-(2k-1)x+k2-1=0根的情况是无实数根.
已知反比例函数y=$\frac{k-2}{x}$的图象如图,则一元二次方程x2-(2k-1)x+k2-1=0根的情况是无实数根.
分析 首先根据反比例函数的性质求得k的取值范围,从而利用根的判别式确定方程的根的情况即可.
解答 解:∵反比例函数y=$\frac{k-2}{x}$的图象位于第一、第三象限,
∴k-2>0,
解得:k>2,
∴关于x的一元二次方程x2-(2k-1)x+k2-1=0根中△=(2k-1)2-4(k2-1)=-4k+5<0,
∴方程无实数根,
故答案为:无实数根.
点评 本题考查了反比例函数的性质及根的判别式的知识,解题的关键是能够根据反比例函数的性质确定k的取值范围,难度不大.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
14.下列图形中既是中心对称图形,又是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
15.下列函数的解析式中是一次函数的是( )
| A. | y=$\frac{-8}{x}$ | B. | y=-$\frac{1}{5}$x+6 | C. | y=2x2+1 | D. | y=2$\sqrt{x}$+1 |
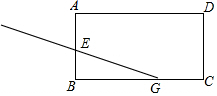 如图,在矩形ABCD中,BG=10,BC=13,将纸片沿过点G的折痕GE折叠,使顶点B的对称点F落在边AD上,折痕与矩形的边交于点E,若满足条件的F点有2个时,AB的取值范围$\sqrt{91}$≤AB<10..
如图,在矩形ABCD中,BG=10,BC=13,将纸片沿过点G的折痕GE折叠,使顶点B的对称点F落在边AD上,折痕与矩形的边交于点E,若满足条件的F点有2个时,AB的取值范围$\sqrt{91}$≤AB<10..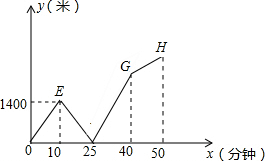 如图,小明和小亮同时从学校放学,两人以各自速度匀速步行回家,小明的家在学校的正西方向,小亮的家在学校的正东方向,小明准备一回家就开始做作业,打开书包时发现错拿了小亮的练习册,于是立即跑步去追小亮,终于在途中追上了小亮并交还了练习册,然后再以先前的速度步行回家,(小明在家中耽搁和交还作业的时间忽略不计)结果小明比小亮晚回到家中.如图是两人之间的距离y米与他们从学校出发的时间x分钟的函数关系图.则小明的家和小亮的家相距2975米.
如图,小明和小亮同时从学校放学,两人以各自速度匀速步行回家,小明的家在学校的正西方向,小亮的家在学校的正东方向,小明准备一回家就开始做作业,打开书包时发现错拿了小亮的练习册,于是立即跑步去追小亮,终于在途中追上了小亮并交还了练习册,然后再以先前的速度步行回家,(小明在家中耽搁和交还作业的时间忽略不计)结果小明比小亮晚回到家中.如图是两人之间的距离y米与他们从学校出发的时间x分钟的函数关系图.则小明的家和小亮的家相距2975米.