题目内容
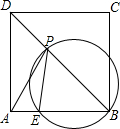 如图,正方形ABCD中,AB=4,AE=1,点P是对角线BD上一动点,当△APE的周长最小时,过B,P,E三点的圆的直径为
如图,正方形ABCD中,AB=4,AE=1,点P是对角线BD上一动点,当△APE的周长最小时,过B,P,E三点的圆的直径为考点:三角形的外接圆与外心,正方形的性质,轴对称-最短路线问题
专题:
分析:连接AC,由正方形的性质可知A和C关于BD对称,再连接CE交BD为P,则此时三角形APE的周长最小,求出P的坐标,即可求出答案.
解答:解:连接AC,连接CE交BD为P,如图所示建立平面直角坐标系,过P作PN⊥x轴于N,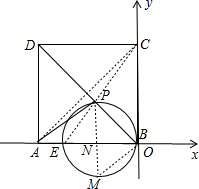
∵四边形ABCD是正方形,
∴直线BD是正方形的一条对称轴,
∴此时三角形APE的周长最小,
∵AE=1,AB=BC=4,
∴BE=3,
由题意知:C(0,4),B(0,0),D(-4,4),E(-3,0),
设P的坐标为(x,y),
设直线BD的解析式为y=kx,
把D(-4,4)代入得:4=-4k,
解得:k=-1,
即y=-x,
∴∠PBA=45°,∠BPN=45°,
∴BN=PN,
作BM⊥PB交圆于M,
则PM为圆的直径,
∠MBN=∠NMB=45°,
∴PM=2PN,
设直线CE的解析式是y=ax+c,
把C(0,4),E(-3,0)代入得:
,
解得:a=
,c=4,
即直线CE的解析式是y=
x+4,
解方程组
得:
,
即P的坐标是(-
,
),
∴PN=
,
∴PM=2PN=
,
故答案为:
.

∵四边形ABCD是正方形,
∴直线BD是正方形的一条对称轴,
∴此时三角形APE的周长最小,
∵AE=1,AB=BC=4,
∴BE=3,
由题意知:C(0,4),B(0,0),D(-4,4),E(-3,0),
设P的坐标为(x,y),
设直线BD的解析式为y=kx,
把D(-4,4)代入得:4=-4k,
解得:k=-1,
即y=-x,
∴∠PBA=45°,∠BPN=45°,
∴BN=PN,
作BM⊥PB交圆于M,
则PM为圆的直径,
∠MBN=∠NMB=45°,
∴PM=2PN,
设直线CE的解析式是y=ax+c,
把C(0,4),E(-3,0)代入得:
|
解得:a=
| 4 |
| 3 |
即直线CE的解析式是y=
| 4 |
| 3 |
解方程组
|
|
即P的坐标是(-
| 12 |
| 7 |
| 12 |
| 7 |
∴PN=
| 12 |
| 7 |
∴PM=2PN=
| 24 |
| 7 |
故答案为:
| 24 |
| 7 |
点评:本题考查了用待定系数法求一次函数的解析式,轴对称-最短路线问题,正方形性质,圆周角定理等知识点的应用,题目比较好,但是难度偏大.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
 如图,用一根长40cm的铁丝围成一个长方形,若长方形的宽比长少2cm,则这个长方形的面积为( )
如图,用一根长40cm的铁丝围成一个长方形,若长方形的宽比长少2cm,则这个长方形的面积为( )| A、90cm2 |
| B、96cm2 |
| C、99cm2 |
| D、100cm2 |
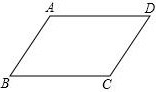 已知:如图,在四边形ABCD中,AB∥CD,∠B=∠D.求证:AD∥BC(用两种不同的方法证明)
已知:如图,在四边形ABCD中,AB∥CD,∠B=∠D.求证:AD∥BC(用两种不同的方法证明) 如图,正方形OABC中顶点B在一双曲线上,请在图中画出一条过点B的直线,使之与双曲线的另一支交于点D,且满足线段BD最短.
如图,正方形OABC中顶点B在一双曲线上,请在图中画出一条过点B的直线,使之与双曲线的另一支交于点D,且满足线段BD最短. 如图,两同心圆的圆心为A,大圆的弦AB切小圆于P,两圆的半径分别为2和1.若用阴影部分围成一个圆锥,则该圆锥的底面半径为
如图,两同心圆的圆心为A,大圆的弦AB切小圆于P,两圆的半径分别为2和1.若用阴影部分围成一个圆锥,则该圆锥的底面半径为