题目内容
18.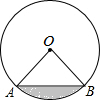 如图,已知⊙O的周长为4π,$\widehat{AB}$的长为π,则图中阴影部分的面积为( )
如图,已知⊙O的周长为4π,$\widehat{AB}$的长为π,则图中阴影部分的面积为( )| A. | π-2 | B. | π-$\sqrt{3}$ | C. | π | D. | 2 |
分析 首先根据⊙O的周长为4π,求出⊙O的半径是多少;然后根据$\widehat{AB}$的长为π,可得$\widehat{AB}$的长等于⊙O的周长的$\frac{1}{4}$,所以∠AOB=90°;最后用⊙O的面积的$\frac{1}{4}$减去△AOB的面积,求出图中阴影部分的面积为多少即可.
解答 解:∵⊙O的周长为4π,
∴⊙O的半径是r=4π÷2π=2,
∵$\widehat{AB}$的长为π,
∴$\widehat{AB}$的长等于⊙O的周长的$\frac{1}{4}$,
∴∠AOB=90°,
∴S阴影=$\frac{1}{4}×π{×2}^{2}-2×2÷2$=π-2.
故选:A.
点评 此题主要考查了扇形面积的计算,以及弧长的计算方法,要熟练掌握,解答此题的关键是要明确求阴影面积常用的方法:①直接用公式法;②和差法;③割补法.

练习册系列答案
相关题目
9.下列一元二次方程两实数根和为4的是( )
| A. | x2+2x-4=0 | B. | x2+2x+10=0 | C. | x2-4x+4=0 | D. | x2+4x-5=0 |
3.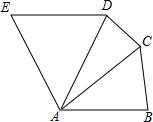 如图,在五边形ABCDE中,AB=AC=AD=AE,且AB∥ED,∠EAB=120°,则∠DCB=( )
如图,在五边形ABCDE中,AB=AC=AD=AE,且AB∥ED,∠EAB=120°,则∠DCB=( )
 如图,在五边形ABCDE中,AB=AC=AD=AE,且AB∥ED,∠EAB=120°,则∠DCB=( )
如图,在五边形ABCDE中,AB=AC=AD=AE,且AB∥ED,∠EAB=120°,则∠DCB=( )| A. | 150° | B. | 160° | C. | 130° | D. | 60° |
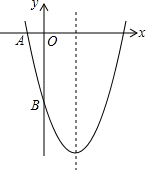 如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A(-1,0)和点B(0,-5).
如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A(-1,0)和点B(0,-5).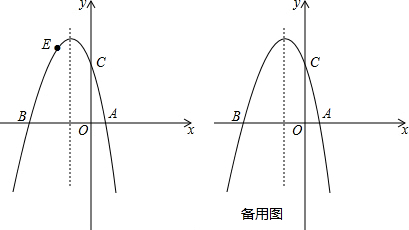
 在平行四边形ABCD中,如果点E是CD的中点,点F是BC边上的一点,且∠FAE=∠EAD,求证:EF⊥AE.
在平行四边形ABCD中,如果点E是CD的中点,点F是BC边上的一点,且∠FAE=∠EAD,求证:EF⊥AE.