题目内容
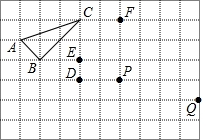 如图,在正方形格纸中,△ABC的三个顶点及D、E、F、P、Q五个点分别位于边长为1的小正方形的顶点上,先从P、Q两个点中任意取一个点,再从D、E、F三个点中任意取两个点,以所取的这三个点为顶点组成三角形,求所组成的三角形与△ABC相似的概率(用画树状图或列表法求解).
如图,在正方形格纸中,△ABC的三个顶点及D、E、F、P、Q五个点分别位于边长为1的小正方形的顶点上,先从P、Q两个点中任意取一个点,再从D、E、F三个点中任意取两个点,以所取的这三个点为顶点组成三角形,求所组成的三角形与△ABC相似的概率(用画树状图或列表法求解).考点:列表法与树状图法,相似三角形的判定
专题:
分析:首先根据题意画出树状图,然后由树状图求得所有等可能的结果与所组成的三角形与△ABC相似的情况,再利用概率公式即可求得答案.
解答:解:画树状图得:

∵△ABC的三边长分别为:AB=
,BC=2
,AC=
,
∴∠ABC=90°,
∵共有6种等可能的结果,所组成的三角形与△ABC相似的有2个,即△PDE和△QEF,
∴所组成的三角形与△ABC相似的概率为:
=
.

∵△ABC的三边长分别为:AB=
| 2 |
| 2 |
| 10 |
∴∠ABC=90°,
∵共有6种等可能的结果,所组成的三角形与△ABC相似的有2个,即△PDE和△QEF,
∴所组成的三角形与△ABC相似的概率为:
| 2 |
| 6 |
| 1 |
| 3 |
点评:此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
方程3x(x-4)=4(x-4)的根为( )
A、x=
| ||
| B、x=4 | ||
C、x1=
| ||
| D、全体实数 |