题目内容
17.已知实数a,b满足(2a+1)2+|a+b+1|=0,且关于x,y的方程组$\left\{\begin{array}{l}{ax+by=m}\\{2ax-by=m+1}\end{array}\right.$的解x<0,y>0,求m的取值范围.分析 根据偶次方,绝对值得出2a+1=0,a+b+1=0,求出a、b的值,代入方程组得出关于x、y的方程组,求出法则的解,根据x<0,y>0得出关于m的不等式组,求出不等式组的解集即可.
解答 解:∵(2a+1)2+|a+b+1|=0,
∴2a+1=0,a+b+1=0,
解得:a=-$\frac{1}{2}$,b=-$\frac{1}{2}$,
代入方程组$\left\{\begin{array}{l}{ax+by=m}\\{2ax-by=m+1}\end{array}\right.$得:$\left\{\begin{array}{l}{-\frac{1}{2}x-\frac{1}{2}y=m}\\{-x+\frac{1}{2}y=m+1}\end{array}\right.$,
解得:x=$\frac{-2(2m+1)}{3}$,y=$\frac{2(1-m)}{3}$,
,∵x<0,y>0,
∴$\left\{\begin{array}{l}{\frac{-2(2m+1)}{3}<0}\\{\frac{2(1-m)}{3}>0}\end{array}\right.$,
解不等式组得:-$\frac{1}{2}$<m<1,
即m的取值范围是:-$\frac{1}{2}$<m<1.
点评 本题考查了偶次方,绝对值的非负性,二元一次方程组的解,解二元一次方程组,解不等式组的应用,解此题的关键是得出关于m的不等式组,综合性比较强.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
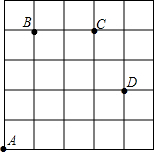 如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向.
如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向. 如图,在平面直角坐标中,一直线与x轴相交于点A(8,0),与y轴交于B(0,6),P是线段AB上一动点(不与A,B重合),过P分别作出x轴和y轴的垂线,垂足为M,N.
如图,在平面直角坐标中,一直线与x轴相交于点A(8,0),与y轴交于B(0,6),P是线段AB上一动点(不与A,B重合),过P分别作出x轴和y轴的垂线,垂足为M,N.