题目内容
如图,AB是⊙O的直径,CD与⊙O相切于点C,DA⊥AB,DO及DO的延长线与⊙O分别相交于点E、F,EB与CF相交于点G.
(1)求证:DA=DC;
(2)⊙O的半径为3,AC=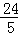 ,求GC的长.
,求GC的长.
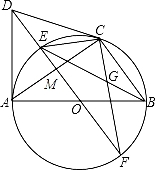
【考点】切线的性质;全等三角形的判定与性质;相似三角形的判定与性质.
【分析】(1)由AB是⊙O的直径,AB⊥DA,可得AD是⊙O的切线,又由DC是⊙O切线,根据切线长定理即可求得答案;
(2)由勾股定理求出EG、CF、BC长,根据△BGC∽△FGE求出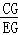 =
=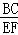 =
= =
=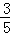 ,则CG=
,则CG=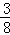 CF;利用勾股定理求出CF的长,则CG的长度可求得.
CF;利用勾股定理求出CF的长,则CG的长度可求得.
【解答】(1)证明:∵AB是⊙O的直径,AB⊥DA,
∴AD是⊙O的切线,
∵DC是⊙O切线,
∴DA=DC.
(2)解:由切线长定理得:DO垂直平方AC,
∵AC=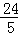 ,
,
∴AM=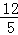 ,
,
在RT△MAO中,OM=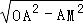 =
= =
=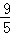 ,
,
∴EM=3﹣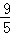 =
=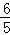 ,
,
在RT△EMC中,CE=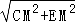 =
=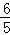
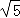 ,
,
∵EF是直径,
∴∠ECF=90°,
∴CF=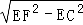 =
=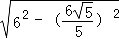 =
=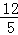
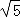 ,
,
∵AB是直径,
∴∠ACB=90°,
∴BC=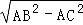 =
=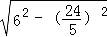 =
=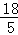 ,
,
∵∠GCB=∠GEF,∠GFE=∠GBC,(圆周角定理)
∴△BGC∽△FGE,
∴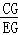 =
=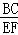 =
= =
=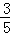 ,
,
∵CF=CG+GF,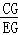 =
=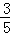 ,
,
∴CG=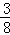 CF=
CF=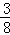 ×
×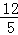
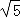 =
=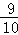
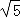 .
.
【点评】本题考查了切线的判定和性质,切线长定理,勾股定理,相似三角形的性质和判定,圆周角定理等知识点的应用,主要考查学生综合运用定理进行推理和计算的能力,综合性比较强,难度偏大.

练习册系列答案
相关题目