Question

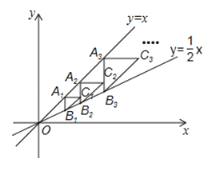
【题目】如图，点A1（2，2）在直线y＝x上，过点A1作A1B1∥y轴交直线y＝x于点B1，以点A1为直角顶点，A1B1为直角边在A1B1的右侧作等腰直角△A1B1C1，再过点C1作A2B2∥y轴，分别交直线y＝x和y＝x于A2，B2两点，以点A2为直角顶点，A2B2为直角边在A2B2的右侧作等腰直角△A2B2C2…，按此规律进行下去，则等腰直角△A8B8C8的面积为_____．

Answer 1

【答案】

【解析】

先根据点的坐标以及∥y轴，求得的坐标，进而得到的长以及△面积，再根据的坐标以及∥y轴，求得的坐标，进而得到的长以及△面积，最后根据根据变换规律，求得的长，得出△的面积，进而得出△ 的面积．

解：当x=2时，y=即

∴即△的面积=

∵ ∴

又∵∥y轴，交直线点，

∴ ∴

span>即△面积= ；

以此类推，

即△面积=

即△面积=

…

∴，故△的面积＝

当故△的面积＝

故答案为：