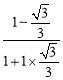Question

【题目】已知⊙O的半径为3，△ABC是⊙O的内接三角形且AB=3，则∠ACB的度数为__________．

Answer 1

【答案】45°或135°

【解析】

当点C在优弧AB时，如图，连接BO并延长，交⊙O于点E，连接BE，由⊙O的半径为3，得到BE＝6，∠BAE＝90°，解直角三角形并利用圆周角定理即可得到结论；当点C（即图中）在劣弧AB时，根据圆内接四边形的性质即可得到结论．

解：当点C在优弧AB时，如图，连接BO并延长，交⊙O于点E，连接BE

∵⊙O的半径为3，

∴BE＝6，∠BAE＝90°，

∵AB＝3，

∴AE＝ ＝3，

∴是等腰直角三角形，

∴∠E＝45°，

∴∠C=∠E＝45°；

当点C（即图中）在劣弧AB时，

∠C′＝180°﹣45°＝135°；

综上所述，∠ACB的度数为45°或135°，

故答案为：45°或135°．