题目内容
 已知如图,直线y=
已知如图,直线y=| 4 |
| 3 |
(1)直接写出当t=0.5时,P、Q两点的坐标;
(2)试探究:在整个运动过程中,直线MN与菱形的边有公共点的时间有多长?
(3)当直线MN与菱形的边有公共点时,以PQ为直径的圆能否与菱形的边AB所在直线相切?如能,求出此时t的值;如不能,说明理由.
考点:一次函数综合题
专题:
分析:(1)根据平移的规律“上加下减”写出直线PQ的解析式,根据解析式来求P、Q两点的坐标;
(2)直线MN与菱形的边有公共点的时间段为:点Q与菱形ABCD的顶点A重合到点Q与顶点C重合这一时间段.此题为追击问题.根据“点Q与点A、C的运动时间相等”列出关于t的方程,通过方程来解答问题;
(3)分①当Q在x轴上方;②当Q在x轴下方;两种情况讨论可得以PQ为直径的圆能与菱形的边AB所在直线相切时t的值.
(2)直线MN与菱形的边有公共点的时间段为:点Q与菱形ABCD的顶点A重合到点Q与顶点C重合这一时间段.此题为追击问题.根据“点Q与点A、C的运动时间相等”列出关于t的方程,通过方程来解答问题;
(3)分①当Q在x轴上方;②当Q在x轴下方;两种情况讨论可得以PQ为直径的圆能与菱形的边AB所在直线相切时t的值.
解答:解:(1)∵直线MN沿着y轴的负方向以每秒4个单位的速度匀速运动,
∴t=0.5时,直线MN在y的负方向上移动的距离是:4×0.5=2.
则直线MN平移后的解析式为:y=
x+8-2=
x+6,即y=
x+6.
则当x=0时,y=6.
当y=0时,x=-
.
所以P(-
,0),Q(0,6);
(2)∵直线MN的解析式为y=
x+8,
∴M(0,8),
又∵在菱形ABCD中,点A坐标为(0,4),则点C的坐标是(0,-4),
∴OA=4,OM=8,CM=12.
当点Q与顶点A重合时,4t-t=4,
解得 t=
(秒).
当点Q与顶点C重合时,4t-t=12,
解得 t=4,
∴4-
=
(秒)
故直线MN与菱形的边有公共点的时间有
秒;
(3)当MN与菱形有交点,AQ=3t-4,
∵A(0,4),B(-3,0),
∴OA=4,OB=3,
∴AB=5,
∴sin∠BAO=
,
∴QE=
(3t-4),
①当Q在x轴上方,
∵PO=6-3t,OQ=8-4t,
∴PQ=10-5t,
(10-5t)÷2=
(3t-4),
解得t=
;
②当Q在x轴下方,
PQ=5t-10,
(5t-10)÷2=
(3t-4),
解得t=
.
综上所述,t=
或
时,以PQ为直径的圆能与菱形的边AB所在直线相切.
∴t=0.5时,直线MN在y的负方向上移动的距离是:4×0.5=2.
则直线MN平移后的解析式为:y=
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
则当x=0时,y=6.
当y=0时,x=-
| 9 |
| 2 |
所以P(-
| 9 |
| 2 |
(2)∵直线MN的解析式为y=
| 4 |
| 3 |
∴M(0,8),
又∵在菱形ABCD中,点A坐标为(0,4),则点C的坐标是(0,-4),

∴OA=4,OM=8,CM=12.
当点Q与顶点A重合时,4t-t=4,
解得 t=
| 4 |
| 3 |
当点Q与顶点C重合时,4t-t=12,
解得 t=4,
∴4-
| 4 |
| 3 |
| 8 |
| 3 |
故直线MN与菱形的边有公共点的时间有
| 8 |
| 3 |
(3)当MN与菱形有交点,AQ=3t-4,
∵A(0,4),B(-3,0),
∴OA=4,OB=3,
∴AB=5,
∴sin∠BAO=
| 3 |
| 5 |
∴QE=
| 3 |
| 5 |
①当Q在x轴上方,
∵PO=6-3t,OQ=8-4t,
∴PQ=10-5t,
(10-5t)÷2=
| 3 |
| 5 |
解得t=
| 74 |
| 43 |
②当Q在x轴下方,
PQ=5t-10,
(5t-10)÷2=
| 3 |
| 5 |
解得t=
| 26 |
| 7 |
综上所述,t=
| 74 |
| 43 |
| 26 |
| 7 |
点评:考查了一次函数综合题,涉及了一次函数平移的规律,菱形的性质,切线的判定及性质及方程思想、分类思想的运用,综合性较强,有一定的难度.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
如图图形中,是轴对称图形但不是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
已知3m-5和-2m+3互为相反数,则m的值为( )
A、
| ||
| B、8 | ||
| C、2 | ||
| D、-8 |
 如图,一次函数y=2x-6与反比例函数y=
如图,一次函数y=2x-6与反比例函数y= 如图,已知平面直角坐标内有三点,分别为A(-1,1),B(-2,4),C(-3,2).
如图,已知平面直角坐标内有三点,分别为A(-1,1),B(-2,4),C(-3,2).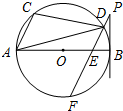 如图,AB是⊙O的直径,点A、C、D在⊙O上,BP是⊙O的切线,连接PD并延长交⊙O于F、交AB于E,若∠BPF=∠ADC.
如图,AB是⊙O的直径,点A、C、D在⊙O上,BP是⊙O的切线,连接PD并延长交⊙O于F、交AB于E,若∠BPF=∠ADC.