题目内容
12.(1)用简便方法计算:20082-4016×2001+20012(2)先化简,再求值:($\frac{a}{b}$-$\frac{b}{a}$)÷$\frac{{a}^{2}+ab}{{a}^{2}b}$,其中a=-$\frac{1}{3}$,b=-$\frac{1}{2}$.
分析 (1)观察可得原式可整理得:20082-2×2008×2001+20012,2008和2001两数的平方和减去他们它们乘积的2倍,符合完全平方公式结构特征,因此可应用完全平方公式进行计算;
(2)先根据分式混合运算的法则把原式进行化简,再把a=-$\frac{1}{3}$,b=-$\frac{1}{2}$代入进行计算即可.
解答 解:(1)原式=20082-2×2008×2001+20012
=(2008-2001)2
=72
=49;
(2)原式=$\frac{(a+b)(a-b)}{ab}$÷$\frac{a(a+b)}{{a}^{2}b}$
=$\frac{(a+b)(a-b)}{ab}$•$\frac{ab}{a+b}$
=a-b,
当a=-$\frac{1}{3}$,b=-$\frac{1}{2}$时,原式=$\frac{1}{6}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
3.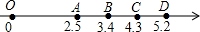 如图,在数轴上有标有O,A,B,C,D五个点,根据图中各点所表示的数,$\sqrt{12}$在线段( )
如图,在数轴上有标有O,A,B,C,D五个点,根据图中各点所表示的数,$\sqrt{12}$在线段( )
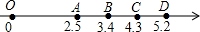 如图,在数轴上有标有O,A,B,C,D五个点,根据图中各点所表示的数,$\sqrt{12}$在线段( )
如图,在数轴上有标有O,A,B,C,D五个点,根据图中各点所表示的数,$\sqrt{12}$在线段( )| A. | OA上 | B. | AB上 | C. | BC上 | D. | CD上 |
17.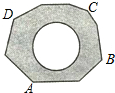 如图,地面上有一个不规则的封闭图形ABCD,为求得它的面积,小明在此封闭图形内画出一个半径为1米的圆后,在附近闭上眼睛向封闭图形内掷小石子(可把小石子近似地看成点),记录如下:
如图,地面上有一个不规则的封闭图形ABCD,为求得它的面积,小明在此封闭图形内画出一个半径为1米的圆后,在附近闭上眼睛向封闭图形内掷小石子(可把小石子近似地看成点),记录如下:
(1)当投掷的次数很大时,则m:n的值越来越接近0.5;
(2)若以小石子所落的有效区域为总数(即m+n),则随着投掷次数的增大,小石子落在圆内(含圆上)的频率值稳定在$\frac{1}{3}$;
(3)请你利用(2)中所得频率的值,估计整个封闭图形ABCD的面积是3π米2(结果保留π)
 如图,地面上有一个不规则的封闭图形ABCD,为求得它的面积,小明在此封闭图形内画出一个半径为1米的圆后,在附近闭上眼睛向封闭图形内掷小石子(可把小石子近似地看成点),记录如下:
如图,地面上有一个不规则的封闭图形ABCD,为求得它的面积,小明在此封闭图形内画出一个半径为1米的圆后,在附近闭上眼睛向封闭图形内掷小石子(可把小石子近似地看成点),记录如下: | 50 | 50 | 300 | … |
| 石子落在圆内(含圆上)次数m | 14 | 48 | 89 | … |
| 石子落在圆以外的阴影部分(含外缘上)次数n | 30 | 95 | 180 | … |
(2)若以小石子所落的有效区域为总数(即m+n),则随着投掷次数的增大,小石子落在圆内(含圆上)的频率值稳定在$\frac{1}{3}$;
(3)请你利用(2)中所得频率的值,估计整个封闭图形ABCD的面积是3π米2(结果保留π)
4.下面是由数字组成的4个图形,其中能看到轴对称的图形的有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,在半径为5$\sqrt{2}$的⊙O中,弦AB、CD互相垂直,若AB=14,CD=10,则BC的长为6$\sqrt{5}$.
如图,在半径为5$\sqrt{2}$的⊙O中,弦AB、CD互相垂直,若AB=14,CD=10,则BC的长为6$\sqrt{5}$.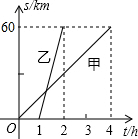 A,B两地相距60km.甲、乙二人分别骑自行车和摩托车沿相同路线匀速行驶,由A地到达B地,他们行驶的路程s(km)与甲出发后的时间t(h)之间的函数图象如图所示
A,B两地相距60km.甲、乙二人分别骑自行车和摩托车沿相同路线匀速行驶,由A地到达B地,他们行驶的路程s(km)与甲出发后的时间t(h)之间的函数图象如图所示