题目内容
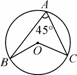
如图15,从一个直径为4的圆形铁片中剪下一个圆心角为90°的扇形ABC.
(1)求这个扇形的面积;
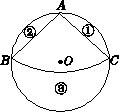
(2)在剩下的材料中,能否从③中剪出一个圆作为底面,与扇形ABC围成一个圆锥?若不能,请说明理由;若能,请求出剪的圆的半径是多少.
解:(1)如答图7所示,连接BC.
由∠BAC=90°得BC为⊙O的直径,
∴BC=4.
在Rt△ABC中,由勾股定理可得:AB=AC=2 ,
,
∴S扇形ABC=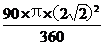 =2π.
=2π.
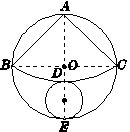
答图7
(2)不能.
如答图7所示,连接AO并延长交⌒BC于点D,交⊙O于点E,则
DE=4-2 .
.
而l⌒BC=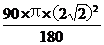 =
= π,
π,
设能与扇形ABC围成圆锥的底面圆的直径为d,
则dπ= π,
π,
∴d= .
.
又∵DE=4-2 <d=
<d= ,即围成圆锥的底面圆的直径大于DE,
,即围成圆锥的底面圆的直径大于DE,
∴不能围成圆锥.
点拨:(1)由勾股定理求出扇形的半径,再根据扇形面积公式求值.(2)题需要求出③中最大圆的直径以及圆锥底面圆的直径(圆锥底面圆的周长即为弧BC的长),然后进行比较即可.

练习册系列答案
相关题目




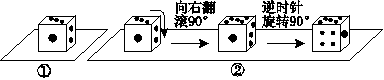
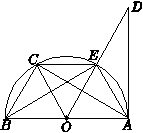
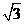 为半径的圆在运动过程中与△ABC的边第二次相切时是出发后第________秒.
为半径的圆在运动过程中与△ABC的边第二次相切时是出发后第________秒.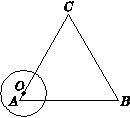
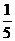 B.
B.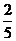 C.
C. D.
D.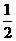

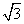 cm B.2
cm B.2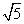 cm C.
cm C. cm D.
cm D.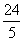 cm
cm