题目内容
20. 我们把两组邻边相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AB=CB,AD=CD.对角线AC,BD相交于点O,OE⊥AB,OF⊥CB,垂足分别是E,F.求证OE=OF.
我们把两组邻边相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AB=CB,AD=CD.对角线AC,BD相交于点O,OE⊥AB,OF⊥CB,垂足分别是E,F.求证OE=OF.
分析 欲证明OE=OF,只需推知BD平分∠ABC,所以通过全等三角形△ABD≌△CBD(SSS)的对应角相等得到∠ABD=∠CBD,问题就迎刃而解了.
解答 证明:∵在△ABD和△CBD中,$\left\{\begin{array}{l}AB=CB\\ AD=CD\\ BD=BD\end{array}\right.$,
∴△ABD≌△CBD(SSS),
∴∠ABD=∠CBD,
∴BD平分∠ABC.
又∵OE⊥AB,OF⊥CB,
∴OE=OF.
点评 本题考查了全等三角形的判定与性质.在应用全等三角形的判定时,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形.

练习册系列答案
相关题目
15.已知x=2-$\sqrt{3}$,则代数式(7+4$\sqrt{3}$)x2+(2+$\sqrt{3}$)x+$\sqrt{3}$的值是( )
| A. | 0 | B. | $\sqrt{3}$ | C. | 2+$\sqrt{3}$ | D. | 2-$\sqrt{3}$ |
5. 如图,BC⊥AE于点C,CD∥AB,∠B=40°,则∠ECD的度数是( )
如图,BC⊥AE于点C,CD∥AB,∠B=40°,则∠ECD的度数是( )
 如图,BC⊥AE于点C,CD∥AB,∠B=40°,则∠ECD的度数是( )
如图,BC⊥AE于点C,CD∥AB,∠B=40°,则∠ECD的度数是( )| A. | 70° | B. | 60° | C. | 50° | D. | 40° |
14. 如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x袖于点M,交y轴于点N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为( )
如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x袖于点M,交y轴于点N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为( )
 如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x袖于点M,交y轴于点N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为( )
如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x袖于点M,交y轴于点N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为( )| A. | a-b | B. | 2a+b=-1 | C. | 2a-b=l | D. | 2a+b=l |
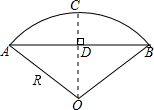 赵州桥是我国建筑史上的一大创举,它距今约1400年,历经无数次洪水冲击和8次地震却安然无恙.如图,若桥跨度AB约为40米,主拱高CD约10米,则桥弧AB所在圆的半径R=25米.
赵州桥是我国建筑史上的一大创举,它距今约1400年,历经无数次洪水冲击和8次地震却安然无恙.如图,若桥跨度AB约为40米,主拱高CD约10米,则桥弧AB所在圆的半径R=25米.