题目内容
8.已知实数a,b满足a-b=1,a2-ab+2>0,当1≤x≤2时,函数y=$\frac{a}{x}$(a≠0)的最大值与最小值之差是1,求a的值.分析 首先根据条件a-b=1,a2-ab+2>0可确定a>-2,然后再分情况进行讨论:①当-2<a<0,1≤x≤2时,函数y=$\frac{a}{x}$的最大值是y=$\frac{a}{2}$,最小值是y=a,②当a>0,1≤x≤2时,函数y=$\frac{a}{x}$的最大值是y=a,最小值是y=$\frac{a}{2}$,再分别根据最大值与最小值之差是1,计算出a的值.
解答 解:∵a2-ab+2>0,
∴a2-ab>-2,
a(a-b)>-2,
∵a-b=1,
∴a>-2,
①当-2<a<0,1≤x≤2时,函数y=$\frac{a}{x}$的最大值是y=$\frac{a}{2}$,最小值是y=a,
∵最大值与最小值之差是1,
∴$\frac{a}{2}$-a=1,
解得:a=-2,不合题意,舍去;
②当a>0,1≤x≤2时,函数y=$\frac{a}{x}$的最大值是y=a,最小值是y=$\frac{a}{2}$,
∵最大值与最小值之差是1,
∴a-$\frac{a}{2}$=1,
解得:a=2,符合题意,
∴a的值是2.
点评 此题主要考查了反比例函数的性质,关键是掌握反比例函数$y=\frac{k}{x}$(k≠0),当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小;当k<0,双曲线的两支分别位于第二、第四象限,在每一象限内y随x的增大而增大.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
18.某蔬菜经营户从蔬菜批发市场批发蔬菜进行零售,部分蔬菜批发价格与零售价格如表:
请解答下列问题:
(1)第一天,该经营户批发西红柿和西兰花两种蔬菜共300kg,用去了1520元钱,这两种蔬菜当天全部售完一共能赚多少元钱?
(2)第二天,该经营户用1520元钱仍然批发西红柿和西兰花,要想当天全部售完后所赚钱数不少于1050元,则该经营户最多能批发西红柿多少kg?
| 蔬菜品种 | 西红柿 | 青椒 | 西兰花 | 豆角 |
| 批发价(元/kg) | 3.6 | 5.4 | 8 | 4.8 |
| 零售价(元/kg) | 5.4 | 8.4 | 14 | 7.6 |
(1)第一天,该经营户批发西红柿和西兰花两种蔬菜共300kg,用去了1520元钱,这两种蔬菜当天全部售完一共能赚多少元钱?
(2)第二天,该经营户用1520元钱仍然批发西红柿和西兰花,要想当天全部售完后所赚钱数不少于1050元,则该经营户最多能批发西红柿多少kg?
19.下列各数是无理数的是( )
| A. | $\sqrt{4}$ | B. | $-\frac{1}{3}$ | C. | π | D. | -1 |
16.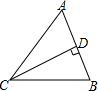 如图,△ABC是锐角三角形,过点C作CD⊥AB,垂足为D,则点C到直线AB的距离是( )
如图,△ABC是锐角三角形,过点C作CD⊥AB,垂足为D,则点C到直线AB的距离是( )
 如图,△ABC是锐角三角形,过点C作CD⊥AB,垂足为D,则点C到直线AB的距离是( )
如图,△ABC是锐角三角形,过点C作CD⊥AB,垂足为D,则点C到直线AB的距离是( )| A. | 线段CA的长 | B. | 线段CD的长 | C. | 线段AD的长 | D. | 线段AB的长 |
13.今年,我省启动了“关爱留守儿童工程”.某村小为了了解各年级留守儿童的数量,对一到六年级留守儿童数量进行了统计,得到每个年级的留守儿童人数分别为10,15,10,17,18,20.对于这组数据,下列说法错误的是( )
| A. | 平均数是15 | B. | 众数是10 | C. | 中位数是17 | D. | 方差是$\frac{44}{3}$ |
 我们把两组邻边相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AB=CB,AD=CD.对角线AC,BD相交于点O,OE⊥AB,OF⊥CB,垂足分别是E,F.求证OE=OF.
我们把两组邻边相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AB=CB,AD=CD.对角线AC,BD相交于点O,OE⊥AB,OF⊥CB,垂足分别是E,F.求证OE=OF.