题目内容
 已知:如图,在△ABC中,∠C=90°,D是AB中点,FD⊥ED于D,BE=
已知:如图,在△ABC中,∠C=90°,D是AB中点,FD⊥ED于D,BE=| 6 |
| 3 |
考点:全等三角形的判定与性质,勾股定理
专题:
分析:延长DE到H,使DH=DE,连接FH,然后利用“边角边”证明△BED和△AHD全等,根据全等三角形对应边相等可得AH=BE,全等三角形对应角相等可得∠B=∠DAH,然后求出∠FAH=90°,再利用勾股定理列式求出FH,然后根据线段垂直平分线上的点到两端点的距离相等可得EF=FH.
解答: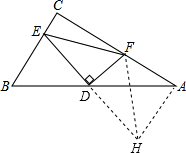 解:如图,延长DE到H,使DH=DE,连接FH,
解:如图,延长DE到H,使DH=DE,连接FH,
∵D是AB中点,
∴AD=BD,
在△BED和△AHD中,
,
∴△BED≌△AHD(SAS),
∴AH=BE=
,∠B=∠DAH,
∵∠C=90°,
∴∠FAH=∠BAC+∠DAH=∠BAC+∠B=180°-90°=90°,
∴由勾股定理得,FH=
=
=3,
∵FD⊥ED,DE=DH,
∴EF=FH=3.
 解:如图,延长DE到H,使DH=DE,连接FH,
解:如图,延长DE到H,使DH=DE,连接FH,∵D是AB中点,
∴AD=BD,
在△BED和△AHD中,
|
∴△BED≌△AHD(SAS),
∴AH=BE=
| 6 |
∵∠C=90°,
∴∠FAH=∠BAC+∠DAH=∠BAC+∠B=180°-90°=90°,
∴由勾股定理得,FH=
| AF2+AH2 |
(
|
∵FD⊥ED,DE=DH,
∴EF=FH=3.
点评:本题考查了全等三角形的判定与性质,勾股定理,线段垂直平分线上的点到两端点的距离相等的性质,作辅助线构造出全等三角形和直角三角形是解题的关键,也是本题的难点.

练习册系列答案
相关题目
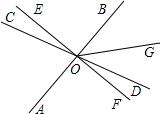 已知,如图,AB、CD、EF三条直线交于点O,且OE⊥AB,∠COE=20°,OG平分∠BOD,则∠DOG的度数是( )
已知,如图,AB、CD、EF三条直线交于点O,且OE⊥AB,∠COE=20°,OG平分∠BOD,则∠DOG的度数是( )| A、20° | B、30° |
| C、35° | D、40° |
下列等式由左边向右边的变形中,属于因式分解的是( )
| A、x2+5x-1=x(x+5)-1 | ||
B、x2+3x-4=x(x+3-
| ||
| C、(x+2)(x-2)=x2-4 | ||
| D、x2-4=(x+2)(x-2) |
 如图,已知CD∥AB,OE平分∠COB,EO⊥FO,∠DCO=60°,求∠COF的度数?
如图,已知CD∥AB,OE平分∠COB,EO⊥FO,∠DCO=60°,求∠COF的度数?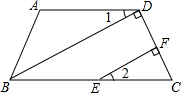 请填写下列证明中的推理依据.
请填写下列证明中的推理依据. 如图,在梯形ABCD中,AD∥BC,∠ADC=90°,∠B=30°,CE⊥AB,垂足为点E.若AD=1,AB=2
如图,在梯形ABCD中,AD∥BC,∠ADC=90°,∠B=30°,CE⊥AB,垂足为点E.若AD=1,AB=2 如图,在8×8的正方形网格中,有Rt△ABC,其顶点都在格点上.
如图,在8×8的正方形网格中,有Rt△ABC,其顶点都在格点上.