Question

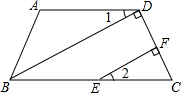
请填写下列证明中的推理依据．
如图所示，四边形ABCD中，∠A=106°-α，∠ABC=74°+α，BD⊥DC于点D，EF⊥DC于点F．求证：∠1=∠2
证明：∵∠A=106°-α，∠ABC=74°+α（已知）
∴∠A+∠ABC=（

 

）°（等式的性质）
∴AD∥BC（

 

 ）
∴∠1=∠DBC（

 

 ）
∵BD⊥DC，EF⊥DC（已知）
∴∠BDF=∠EFC=90°（

 

 ）
∴BD∥EF（

 

 ）
∴∠2=∠DBC（

 

 ）
∴∠1=∠2（等量代换）

Answer 1

考点：平行线的判定与性质

专题：推理填空题

分析：求出∠A+∠ABC=180°，推出AD∥BC，根据平行线的性质求出∠1=∠DBC，根据平行线的判定推出BD∥EF，根据平行线的性质得出∠2=∠DBC，即可得出答案．

解答：证明：∵∠A=106°-α，∠ABC=74°+α，
∴∠A+∠ABC=180°，
∴AD∥BC（同旁内角互补，两直线平行），
∴∠1=∠DBC（两直线平行，内错角相等），
∵BD⊥DC，EF⊥DC，
∴∠BDF=∠EFC=90°（垂直定义），
∴BD∥EF（同位角相等，两直线平行），
∴∠2=∠DBC（两直线平行，同位角相等），
∴∠1=∠2，
故答案为：180，同旁内角互补，两直线平行，两直线平行，内错角相等，垂直定义，同位角相等，两直线平行，两直线平行，同位角相等．

点评：本题考查了平行线的性质和判定的应用，注意：平行线的性质是①两直线平行，同位角相等，②两直线平行，内错角相等，③两直线平行，同旁内角互补，反之亦然．