题目内容
20.已知AB是⊙O的直径.AC、AD是弦,AB=2,AC=$\sqrt{2}$,AD=1,则∠CAD=15°或75°.分析 本题大致的思路是连接BC、BD,分别在Rt△CAB和Rt△BAD中,求出∠CAD和∠CAB的度数,然后根据D点的不同位置分类讨论.
解答 解:本题分两种情况:(如图) ①当AD在AB上方时,连接BD、BC,
①当AD在AB上方时,连接BD、BC,
则∠ADB=∠ACB=90°,
Rt△ADB中,AD=1,AB=2,
∴∠DAB=60°,
Rt△ACB中,AC=$\sqrt{2}$,AB=2,
∴∠CAB45°,
∴∠CAD=∠DAB-∠CAB=15°,
②当AD在AB下方时,同①可求得∠CAD=105°,
故答案为:15°或75°.
点评 本题考查的是圆周角定理及直角三角形的性质,比较简单,但在解答时要注意分两种情况讨论,不要漏解,难度适中.

练习册系列答案
相关题目
8.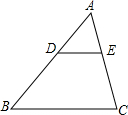 如图,△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,DE=2cm,则BC边的长是( )
如图,△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,DE=2cm,则BC边的长是( )
 如图,△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,DE=2cm,则BC边的长是( )
如图,△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,DE=2cm,则BC边的长是( )| A. | 6cm | B. | 4cm | C. | 8cm | D. | 7cm |
5. 如图,一个长方体的左视图、俯视图,根据图示的数据可计算出主视图的面积为( )
如图,一个长方体的左视图、俯视图,根据图示的数据可计算出主视图的面积为( )
 如图,一个长方体的左视图、俯视图,根据图示的数据可计算出主视图的面积为( )
如图,一个长方体的左视图、俯视图,根据图示的数据可计算出主视图的面积为( )| A. | 12 | B. | 24 | C. | 32 | D. | 48 |
9. 如图所示几何体的俯视图是( )
如图所示几何体的俯视图是( )
 如图所示几何体的俯视图是( )
如图所示几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
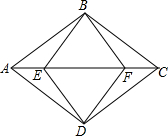 如图,ABCD是平行四边形,E、F是对角线AC上的两点,若∠ABF=∠CDE=90°.
如图,ABCD是平行四边形,E、F是对角线AC上的两点,若∠ABF=∠CDE=90°.