题目内容
14.如果一个数表中某一列各数之和为负数,那么改变该列中所有数的符号,称之为一次“操作”,下表是由8个整数组成的数表,若经过一次“操作”后,使可使新的数表每行的各数之和与每列的各数之和均为非负数,则整数a的值为1或2.| a | a2-1 | -a | -a2 |
| 2-a | 1-a2 | a-2 | a2 |
分析 根据每一列所有数之和分别为2,0,-2,0,每一行所有数之和分别为-1,1,然后分别根据如果操作第三列或第一行,根据每行的各数之和与每列的各数之和均为非负整数,列出不等式组,求出不等式组的解集,即可得出答案.
解答 解:∵每一列所有数之和分别为2,0,-2,0,每一行所有数之和分别为-1,1,则:
如果操作第三列,
| a | a2-1 | a | -a2 |
| 2-a | 1-a2 | 2-a | a2 |
解得:$\frac{1}{2}$≤a≤$\frac{5}{2}$,
又∵a为整数,
∴a=1或a=2.
故答案为:1或2.
点评 此题考查了一元一次不等式组的应用,关键是读懂题意,根据题目中的操作要求,列出不等式组,注意a为整数.

练习册系列答案
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
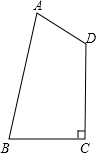 如图,在四边形ABCD中,AB=$\sqrt{5}$,AD=1,BC=CD=$\sqrt{2}$,且∠BCD=90°,试求四边形ABCD的面积.
如图,在四边形ABCD中,AB=$\sqrt{5}$,AD=1,BC=CD=$\sqrt{2}$,且∠BCD=90°,试求四边形ABCD的面积.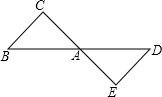 如图,△ABC与△ADE关于点A成中心对称.
如图,△ABC与△ADE关于点A成中心对称.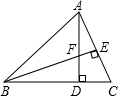 如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为点D,E,AD与BE相交于点F,若BF=AC,则∠ABC=45°.
如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为点D,E,AD与BE相交于点F,若BF=AC,则∠ABC=45°.