题目内容

20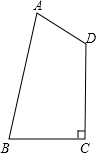．如图，在四边形ABCD中，AB=$\sqrt{5}$，AD=1，BC=CD=$\sqrt{2}$，且∠BCD=90°，试求四边形ABCD的面积．

分析 如图，连接BD．构建直角△ABD、直角△BCD，则四边形ABCD的面积等于图中两直角三角形的面积之和．

解答 解：如图，连接BD，在△ACD中，∠BCD=90°，
由勾股定理得：BD2=CD2+BC2=2．
在△ADB中，∵AD2+BD2=AB2．
由勾股定理的逆定理得：∠ADB=90°，则△ADB是直角三角形，
∴S四边形ABCD=S△ABD+S△BCD
=$\frac{1}{2}$AD•AB+$\frac{1}{2}$BC•CD=2
即四边形ABCD的面积是2．

点评 本题考查了勾股定理在直角三角形中的运用，考查了勾股定理的逆定理的运用，考查了直角三角形面积计算，本题中求证△ACD是直角三角形是解题的关键．

练习册系列答案
相关题目
10．如果3xm+2y3与-2x3y2n-1是同类项，则m、n的值分别是（　　）
A．m=1，n=2B．m=0，n=2C．m=2，n=1D．m=1，n=1
11．如图，已知l1⊥l2，⊙O与l1，l2都相切，⊙O的半径为2cm，矩形ABCD的边AD、AB分别与l1，l2重合，AC=8cm，AD=4cm，若⊙O与矩形ABCD沿l1同时向右移动，⊙O的移动速度为3cm，矩形ABCD的移动速度为4cm/s，设移动时间为t（s）．

（1）如图①，连接OA，则∠OAC的度数为105°；
（2）如图②，两个图形移动一段时间后，⊙O到达⊙O1的位置，矩形ABCD到达A1B1C1D1的位置，此时点O1，A1，C1恰好在同一直线上，求圆心O移动的距离（即OO1的长）；
（3）在移动过程中，圆心O到矩形对角线AC所在直线的距离在不断变化，当直线AC与⊙O第一次相切时，求移动时间t1．（解答时可以利用备用图画出相关示意图）
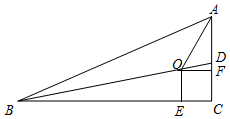8．如图，在Rt△ABC中，∠C=90°，BD是Rt△ABC的一条角平分线，点O、E、F分别在BD、BC、AC上，且四边形OECF是正方形（四边相等，四个角都是直角），
（1）求证：点O在∠BAC的平分线上；
（2）若AC=5，BC=12，AB=13，求OE的长．
15．单项式-3xa-1y4与4x2y2b是同类项，则a+b的值为5．
5．在-8、+3$\frac{1}{2}$、-（-3）、0、-4.2、0.01、-|-2|中，
属于整数集合的有{-8，-（-3），0，-|-2|}；
属于分数集合的有{+3$\frac{1}{2}$，-4.2，0.01　}；
属于正数集合的有{+3$\frac{1}{2}$，0.01}；
属于负数集合的有{-8，-4.2，-|-2|}．
12．已知方程$\frac{x+k}{{x}^{2}-1}$+$\frac{x}{x-1}$=2有增根x=1，则k的值为（　　）
A．-1B．1C．3D．-3
9．在11：20时，时钟上的分针与时针的夹角大小为（　　）
A．120°B．135°C．140°D．150°
14．如果一个数表中某一列各数之和为负数，那么改变该列中所有数的符号，称之为一次“操作”，下表是由8个整数组成的数表，若经过一次“操作”后，使可使新的数表每行的各数之和与每列的各数之和均为非负数，则整数a的值为1或2．
aa2-1-a-a2
2-a1-a2a-2a2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网