题目内容
已知抛物线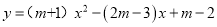 的图象与
的图象与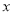 轴有两个公共点.
轴有两个公共点.
(1)求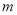 的取值范围,写出当
的取值范围,写出当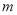 取其范围内最大整数时抛物线的解析式;
取其范围内最大整数时抛物线的解析式;
(2)将(1)中所求得的抛物线记为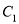 ,
,
①求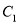 的顶点
的顶点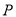 的坐标;
的坐标;
②若当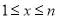 时,
时, 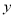 的取值范围是
的取值范围是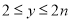 ,求
,求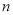 的值;
的值;
(3)将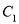 平移得到抛物线
平移得到抛物线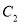 ,使
,使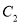 的顶点
的顶点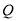 落在以原点为圆心半径为
落在以原点为圆心半径为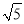 的圆上,求点
的圆上,求点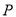 与
与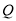 两点间的距离最大时
两点间的距离最大时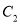 的解析式,怎样平移
的解析式,怎样平移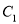 可以得到所求抛物线?
可以得到所求抛物线?

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
题目内容
已知抛物线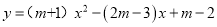 的图象与
的图象与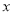 轴有两个公共点.
轴有两个公共点.
(1)求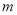 的取值范围,写出当
的取值范围,写出当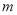 取其范围内最大整数时抛物线的解析式;
取其范围内最大整数时抛物线的解析式;
(2)将(1)中所求得的抛物线记为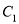 ,
,
①求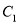 的顶点
的顶点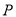 的坐标;
的坐标;
②若当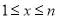 时,
时, 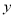 的取值范围是
的取值范围是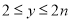 ,求
,求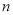 的值;
的值;
(3)将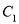 平移得到抛物线
平移得到抛物线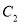 ,使
,使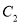 的顶点
的顶点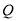 落在以原点为圆心半径为
落在以原点为圆心半径为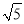 的圆上,求点
的圆上,求点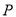 与
与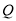 两点间的距离最大时
两点间的距离最大时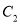 的解析式,怎样平移
的解析式,怎样平移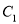 可以得到所求抛物线?
可以得到所求抛物线?

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案