题目内容
17．
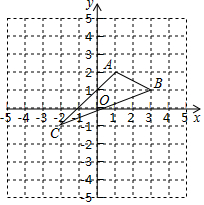在平面直角坐标系中，A（1，2），B（3，1），C（-2，-1）．（1）在图中作出△ABC关于y轴的对称△A1B1C1；
（2）写出对称点A1、B1、C1的坐标；
（3）在y轴上找一点Q，使QA+QB最小．
分析 （1）根据轴对称的性质，作出△ABC关于y轴的对称△A1B1C1；
（2）根据△A1B1C1各顶点的位置，写出其坐标即可；
（3）连接A1B，交y轴于点Q，则QA+QB最小．
解答 解：（1）如图，△A1B1C1即为所求；
（2）由图可得，A1（-1，2）B1（-3，1）C1（2，-1）；
（3）如图，Q点就是所求的点．
点评 本题主要考查了轴对称的性质以及轴对称变换的运用，解决问题时注意：凡是涉及最短距离的问题，一般要考虑线段的性质定理，结合本节所学轴对称变换来解决，多数情况要作点关于某直线的对称点．
练习册系列答案
出彩同步大试卷系列答案
相关题目
8．
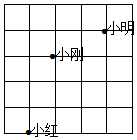如图所示是做课间操时，小明、小红、小刚三人的相对位置，如果用（4，5）表示小明的位置，（2，4）表示小刚的位置，则小红的位置可表示为（ ）
如图所示是做课间操时，小明、小红、小刚三人的相对位置，如果用（4，5）表示小明的位置，（2，4）表示小刚的位置，则小红的位置可表示为（ ）| A． | （0，0） | B． | （0，1） | C． | （1，0） | D． | （1，1） |
5．某超市在“十一”期间对顾客实行优惠购物的条款如下表：
（1）甲顾客一次性购物800元，他实际付款690元．
（2）乙顾客在该超市一次性购物x元，当200≤x＜500时，他实际付款0.9x元；当x≥500时，他实际付款（0.8x+50）元；（用含x的代数式表示）
（3）丙顾客两次购物货款合计为820元，第一次购物的货款为a元（200＜a＜300），试用a的代数式表示丙顾客两次购物实际付款合计多少元？
| 一次性购物 | 优惠办法 |
| 少于200元 | 不予优惠 |
| 低于500元但不低于200元 | 九折优惠 |
| 500元或超过500元 | 其中500元部分给予九折优惠； 超过500元部分给予八折优惠 |
（2）乙顾客在该超市一次性购物x元，当200≤x＜500时，他实际付款0.9x元；当x≥500时，他实际付款（0.8x+50）元；（用含x的代数式表示）
（3）丙顾客两次购物货款合计为820元，第一次购物的货款为a元（200＜a＜300），试用a的代数式表示丙顾客两次购物实际付款合计多少元？
12．
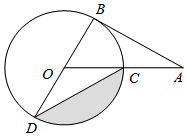如图，AB为⊙O的切线，切点为B，连接AO，OA与⊙O交于点C，BD为⊙O的直径，连接CD，若∠A=30°，⊙O的半径为4，则图中阴影部分的面积为（ ）
如图，AB为⊙O的切线，切点为B，连接AO，OA与⊙O交于点C，BD为⊙O的直径，连接CD，若∠A=30°，⊙O的半径为4，则图中阴影部分的面积为（ ）| A． | $\frac{4}{3}π-\sqrt{3}$ | B． | $\frac{4}{3}π-2\sqrt{3}$ | C． | $4π-4\sqrt{3}$ | D． | $\frac{16}{3}π-4\sqrt{3}$ |
2．二次函数y=（x-1）2-2的顶点坐标是（ ）
| A． | （1，-2） | B． | （-1，2） | C． | （-1，-2） | D． | （1，2） |