题目内容
18.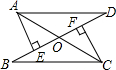 如图,AD=BC,AE,FC都垂直于BD,垂足为E,F,BE=DF,求证:OA=OC.
如图,AD=BC,AE,FC都垂直于BD,垂足为E,F,BE=DF,求证:OA=OC.
分析 根据全等三角形的判定定理AAS证得△AEO≌△CFO;然后由全等三角形的对应边相等即可证得结论.
解答 证明:∵BE=DF,
∴BF=DE,
又∵AE,FC都垂直于BD.
∴∠AED=∠CFB=90°,
在Rt△ADE和Rt△CFB中,
$\left\{\begin{array}{l}{DE=BF}\\{AD=BC}\end{array}\right.$,
∴Rt△ADE≌Rt△CFB(HL),
∴AE=CF(全等三角形的对应边相等).
在△AEO和△CFO中,
$\left\{\begin{array}{l}{∠AOE=∠COF}\\{∠AEO=∠CFO}\\{AE=CF}\end{array}\right.$,
∴△AEO≌△CFO(AAS),
∴OA=OC(全等三角形的对应边相等).
点评 本题考查了全等三角形的判定与性质.解答此类题目,需要利用三角形全等来解决有关边相等的证明.

练习册系列答案
相关题目
 如图,E为△ABC的边BC上一点,D在BA的延长线上,DE交AC于点F,∠B=45°,∠C=30°,∠EFC=70°,求∠D的度数.
如图,E为△ABC的边BC上一点,D在BA的延长线上,DE交AC于点F,∠B=45°,∠C=30°,∠EFC=70°,求∠D的度数. 如图,在10×10正方形网格中,每个小正方形的边长均为1个单位.
如图,在10×10正方形网格中,每个小正方形的边长均为1个单位. 如图,矩形的长为4m,宽为3m,如果将长和宽都增加xm,新矩形的面积为ym2
如图,矩形的长为4m,宽为3m,如果将长和宽都增加xm,新矩形的面积为ym2 已知:如图,CB⊥AD,AE⊥DC,垂足分别B、E,AE、BC相交于点F,且AB=BC.求证:△ABF≌△CBD.
已知:如图,CB⊥AD,AE⊥DC,垂足分别B、E,AE、BC相交于点F,且AB=BC.求证:△ABF≌△CBD.