题目内容
19.如图1是某公园一块草坪上的自动旋转喷水装置,这种旋转喷水装置的旋转角度为240°,它的喷灌区是一个扇形.小涛同学想了解这种装置能够喷灌的草坪面积,他测量出了相关数据,并画出了示意图.如图2,A,B两点的距离为18米,求这种装置能够喷灌的草坪面积.
分析 作OC⊥AB,根据垂径定理得出AC=9,继而可得圆的半径OA的值,再根据扇形面积公式可得答案.
解答 解:过点O作OC⊥AB于C点.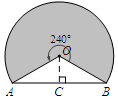
∵OC⊥AB,AB=18,
∴$AC=\frac{1}{2}AB=9$,
∵OA=OB,∠AOB=360°-240°=120°,
∴$∠AOC=\frac{1}{2}∠AOB=60$°.
在Rt△OAC中,OA2=OC2+AC2,
又∵$OC=\frac{1}{2}OA$,
∴$r=OA=6\sqrt{3}$.
∴$S=\frac{240}{360}$πr2=72π(m2).
点评 本题主要考查垂径定理和扇形的面积公式,熟练掌握垂径定理求得圆的半径是解题的关键.

练习册系列答案
相关题目
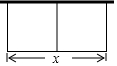 如图,要建一个长方形养鸡场,鸡场的一边靠墙(墙足够长),如果用50m长的篱笆围成中间有一道篱笆墙的养鸡场,设它的长度为x(篱笆墙的厚度忽略不计).
如图,要建一个长方形养鸡场,鸡场的一边靠墙(墙足够长),如果用50m长的篱笆围成中间有一道篱笆墙的养鸡场,设它的长度为x(篱笆墙的厚度忽略不计).