题目内容

18．某商场销售一批衬衫，平均每天可售出20件，每件盈利50元，为了扩大销售，商场决定采取适当的降价措施．经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出2件．若商场平均每天盈利1800元，问每件衬衫应降价多少元？

分析 先设未知数，设每件衬衫应降价x元，则降价后的利润为：（50-x）元，销量增加2x件，一共销（20+2x）件，根据利润=销量×每件衬衫的利润列方程解出即可．

解答 解：设每件衬衫应降价x元，
根据题意得：（50-x）（20+2x）=1800，
解得：x1=x2=20，
答：每件衬衫应降价20元．

点评 此题主要考查了由实际问题抽象出一元二次方程，根据降价后销量的变化得出等式方程是解题关键．

练习册系列答案
相关题目
8．如图，过A（-4，0），$B（0\;，\;\;4\sqrt{3}）$两点的直线与直线y=-$\sqrt{3}$x交于点C，平行于y轴的直线l从原点O出发，以每秒1个单位长度的速度沿戈轴向左平移，到C点时停止．直线l分别交线段BC，OC于点D，E，以DE为边向右侧作等边△DEF．设△DEF与△BCO重叠部分图形的周长为m，直线l的运动时间为t（秒）．
（1）求C点坐标；
（2）当点F落在y轴上时，求相应的时间t的值；
（3）求m与t之间的关系式．【说明：不考虑直线l平移过程中“起点”与“终点”时的情况．】
9．水上游艇是七里海湿地风景区特色旅游项目．如果游客选择此项目，风景区可盈利10元/人．旅游旺季平均每天有500人选择此项目．为增加盈利，景区管理人员准备在旅游旺季提高票价，经调查发现，在其他条件不变的情况下，票价每涨1元，消费人员就减少20人．
（1）现该项目保证每天盈利6000元，同时又要旅游者尽量少花钱，那么票价应涨价多少元？
（2）若单纯从经济角度看，票价涨价多少元，能使该项目获利最多？
6．若a=$\sqrt{6-\sqrt{6-\sqrt{6}-}}$…，b=$\sqrt{2+\sqrt{2+\sqrt{2+…}}}$，则（　　）
A．a=bB．a＞bC．a＜bD．a，b不能比较
13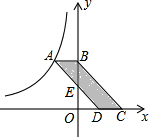．如图，?ABCD的顶点A在反比例函数图象上，边CD落在x轴上，点B在y轴上，AD交y轴于点E，OE：EB=1：2，四边形BCDE的面积为6，则这个反比例函数的解析式是（　　）
A．$y=-\frac{7}{x}$B．$y=-\frac{8}{x}$C．$y=-\frac{9}{x}$D．$y=-\frac{10}{x}$
3．如图，抛物线y=ax2+bx+c经过点A（5，0），B（-3，0），C（0，4）．
（1）求这条抛物线的函数关系式；
（2）过C作CD∥x轴交抛物线于D，连续BC、AD，两个动点P、Q分别从A、B两点同时出发，都以每秒1个单位长度的速度运动．其中，点P沿着线段AB向B点运动，点Q沿着折线B→C→D的路线向D点运动．设这两个动点运动的时间为t（秒）（0＜t＜7），△PQB的面积记为S．
①求S与t的函数关系式；
②当t为何值时，S有最大值，最大值是多少？
③是否存在这样的t值，使得△PQB是直角三角形？若存在，请直接写出t的值；若不存在，请说明理由．
10．小明在做解方程作业时，不小心将方程中的一个常数污染了看不清楚，被污染的方程式2y-$\frac{1}{2}$=$\frac{1}{2}$y+，怎么办呢？小明想了想便翻看书后的答案，得知此方程的解是y=$\frac{7}{3}$，于是很快补好这个常数，这个常数应是（　　）
A．1B．-2C．3D．4
7．已知关于x的一元二次方程（k-2）x2-2x+1=0有两个不相等的实数根，则k的取值范围是（　　）
A．k＜2B．k＜3C．k＜2且k≠0D．k＜3且k≠2
20．直角三角形一条直角边和斜边的长分别是一元二次方程x2-16x+60=0的一个实数根，则该三角形的面积是（　　）
A．24B．24或30C．48D．30

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网