题目内容
8. 如图,过A(-4,0),$B(0\;,\;\;4\sqrt{3})$两点的直线与直线y=-$\sqrt{3}$x交于点C,平行于y轴的直线l从原点O出发,以每秒1个单位长度的速度沿戈轴向左平移,到C点时停止.直线l分别交线段BC,OC于点D,E,以DE为边向右侧作等边△DEF.设△DEF与△BCO重叠部分图形的周长为m,直线l的运动时间为t(秒).
如图,过A(-4,0),$B(0\;,\;\;4\sqrt{3})$两点的直线与直线y=-$\sqrt{3}$x交于点C,平行于y轴的直线l从原点O出发,以每秒1个单位长度的速度沿戈轴向左平移,到C点时停止.直线l分别交线段BC,OC于点D,E,以DE为边向右侧作等边△DEF.设△DEF与△BCO重叠部分图形的周长为m,直线l的运动时间为t(秒).(1)求C点坐标;
(2)当点F落在y轴上时,求相应的时间t的值;
(3)求m与t之间的关系式.【说明:不考虑直线l平移过程中“起点”与“终点”时的情况.】
分析 (1)根据待定系数法求出直线AB的解析式,再利用方程组求出交点坐标C.
(2)设E(t,-$\sqrt{3}$t),则D(-t,-$\sqrt{3}$t+4$\sqrt{3}$),推出DE=-2$\sqrt{3}$t+4$\sqrt{3}$,由△DFE是等边三角形,可得点F坐标(-4t+6,2$\sqrt{3}$),当点F在y轴上时,-4t+6=0,解方程即可解决问题.
(3)分两种情形讨论①当0<t≤1.5时,重叠部分四边形DMNE.②当1.5<t<2时,重叠部分是△DEF.分别计算即可.
解答 解:(1)设直线AB的解析式为y=kx+b则有$\left\{\begin{array}{l}{b=4\sqrt{3}}\\{-4k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\sqrt{3}}\\{b=4\sqrt{3}}\end{array}\right.$,
∴直线AB的解析式为y=$\sqrt{3}$x+4$\sqrt{3}$,
由$\left\{\begin{array}{l}{y=\sqrt{3}x+4\sqrt{3}}\\{y=-\sqrt{3}x}\end{array}\right.$解得$\left\{\begin{array}{l}{x=-2}\\{y=2\sqrt{3}}\end{array}\right.$,
∴点C坐标(-2,2$\sqrt{3}$).
(2)如图1中,作FH⊥DE于H.设E(-t,$\sqrt{3}$t),则D(-t,-$\sqrt{3}$t+4$\sqrt{3}$),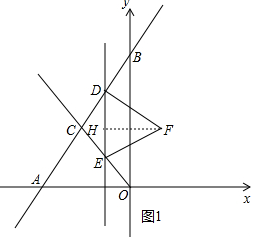
∴DE=-2$\sqrt{3}$t+4$\sqrt{3}$,
∵△DFE是等边三角形,
∴FH=$\frac{\sqrt{3}}{2}$DE=-3t+6,
∴点F坐标(-4t+6,2$\sqrt{3}$),
当点F在y轴上时,-4t+6=0,
∴t=1.5,
∴t=1.5s时,点F在y轴上.
(3)如图2中,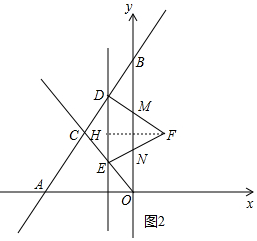
①当0<t≤1.5时,重叠部分四边形DMNE,
m=3(-2$\sqrt{3}$t+4$\sqrt{3}$)-2FM=-6$\sqrt{3}$t+12$\sqrt{3}$-2•$\frac{2\sqrt{3}}{3}$(-4t+6)=-$\frac{2\sqrt{3}}{3}$t+4$\sqrt{3}$.
②当1.5<t<2时,重叠部分是△DEF,
m=3(-2$\sqrt{3}$t+4$\sqrt{3}$)=-6$\sqrt{3}$t+12$\sqrt{3}$.
综上所述,m=$\left\{\begin{array}{l}{-\frac{2\sqrt{3}}{3}t+4\sqrt{3}}&{(0<t≤1.5)}\\{-6\sqrt{3}t+12\sqrt{3}}&{(1.5<t<2)}\end{array}\right.$.
点评 本题考查一次函数综合题、待定系数法、等边三角形的性质、三角形面积等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,属于中考常考题型.

| A. | (20%+x)人 | B. | 20%x人 | C. | (1+20%)x人 | D. | $\frac{x}{1+20%}$人 |
| A. | 一,二,三象限 | B. | 一,二,四象限 | C. | 一,三,四象限 | D. | 二,三,四象限 |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| A. | -1 | B. | 0 | C. | 3 | D. | 1 |
| A. | (2a-b)2=4a2-b2 | B. | (2a-b)(b-2a)=4a2-b2 | ||
| C. | (2a+b)(-2a-b)=4a2-4ab+b2 | D. | (-2a-b)2=4a2+4ab+b2 |
| A. | x+x×5×2.89%=2.1 | B. | x×5×2.89%=21000 | ||
| C. | x×5×2.89%=2.1 | D. | x+x×5×2.89%=21000 |
 如图,已知一次函数y=$\frac{4}{3}$x+m的图象与x轴交于点A(-6,0),交y轴于点B.
如图,已知一次函数y=$\frac{4}{3}$x+m的图象与x轴交于点A(-6,0),交y轴于点B.