题目内容

13．已知2x2-mx-5=（x-1）（2x+n），求m，n的值．

分析 将等式右边展开合并后与等式左边系数对比可得．

解答 解：∵2x2-mx-5=（x-1）（2x+n），
∴2x2-mx-5=（x-1）（2x+n）=2x2+（n-2）x-n
对比系数得：-m=n-2，-5=-n
解得：m=-3，n=5．

点评 本题考查十字相乘法分解因式，根据对应项系数相等列式是求解的关键，明白乘法运算和分解因式是互逆运算．

练习册系列答案
相关题目
3．某商品的标价为200元，8折销售仍赚40元，则商品进价为120元．
4．自2004年5月1日起施行的《中华人民共和国道路交通安全法实施条例》中规定：超速行驶属违法行为．为确保行车安全，某一段全程为200千米的高速公路限速120千米/时（即任意一时刻的车速都不能超过120千米/时）．以下是王师傅和李师傅全程行驶完这线段高速公路时的对话片断．王：“你的车速太快了，平均每小时比我快20千米，比我少用30分钟就行驶完了全程．”李：“虽然我的车速快，但是最快速度比我的平均速度只快15%，并没有超速违法啊．”李师傅超速违法吗？为什么？
1．下列计算正确的是（　　）
A．a2+a2=a4B．2（a-b）=2a-bC．a3•a2=a5D．（-b2）3=-b5
8．已知x-$\frac{1}{x}$=5，则3-$\frac{1}{2}$x2+$\frac{5}{2}$x的值为$\frac{5}{2}$．
18．先化简，再求值：（$\frac{a-1}{a}$-$\frac{a-2}{a+1}$）÷$\frac{2{a}^{2}-a}{{a}^{2}+2a+1}$，其中a满足条件：a2-a-1=0．
5．已知（a+b）2=7，（a-b）2=3，求a2+b2、ab的值．
2．在△ABC中，已知AB=AC、BD是中线，BD把周长分成18cm或20cm两部分，求三边长．
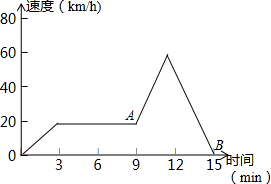2．根据图回答下列问题：
（1）上图反映的是哪两个变量之间的关系？
（2）A、B点分别代表了什么？
（3）说一说速度是怎样随时间变化的？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网