题目内容
2. 已知A(0,4)、B(6,2)表示两个村庄的位置,x轴表示公路的位置,请你在x轴上求一点P,使得AP+BP最小.
已知A(0,4)、B(6,2)表示两个村庄的位置,x轴表示公路的位置,请你在x轴上求一点P,使得AP+BP最小.(1)求P点坐标.
(2)求PA+PB的最小值.
分析 (1)先求出点A关于x轴的对称点A′的坐标,连接A′B交x轴于P,此时PA+PB最小,用待定系数法求出直线A′B的解析式,然后求出直线与x轴的交点即可;
(2)过点B作BC⊥OA,在直角三角形BCA′中利用勾股定理求出A′B的长即可.
解答 解:∵A(0,4),
∴点A关于x轴的对称点A′的坐标为(0,-4),
∵A′(0,-4),B(6,2),
设直线A′B的解析式为y=kx+b(k≠0),
∴$\left\{\begin{array}{l}{2=6k+b}\\{-4=b}\end{array}\right.$,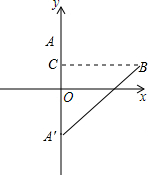
解得$\left\{\begin{array}{l}{k=1}\\{b=-4}\end{array}\right.$,
∴直线A′B的解析式为y=x-4,
当y=0时,x=4.
∴P(4,0);
(2)过点B作BC⊥OA,
∵点B(6,2),
∴CO=2,BC=6,
∴CA′=6,
∴A′B=$\sqrt{{6}^{2}+{6}^{2}}$=6$\sqrt{2}$.
点评 本题考查的是轴对称-最短路线问题以及勾股定理的运用,熟知“两点之间线段最短”是解答此题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
7.如果A是x的二次多项式,B是x的四次多项式,那么A-B是( )
| A. | 三次多项式 | B. | 二次多项式 | C. | 四次多项式 | D. | 五次多项式 |
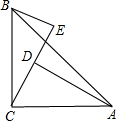 如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于点D,AD=3.1cm,DE=1.8cm,求BE的长.
如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于点D,AD=3.1cm,DE=1.8cm,求BE的长.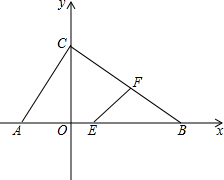 如图,在平面直角坐标系中,△ABC的顶点都在坐标轴上,OA=2,OC=3,OB=4.点E,F分别是线段AB,BC上的动点(不与端点A,B重合),点E从点A出发沿x轴正方向以每秒2个单位长度的速度向点B运动,同时点F从点B出发沿线段BC方向以每秒1个单位长度的速度向点C运动(当点E停止时,点F也同时停止),当两个动点运动了t秒时,解答下列问题:
如图,在平面直角坐标系中,△ABC的顶点都在坐标轴上,OA=2,OC=3,OB=4.点E,F分别是线段AB,BC上的动点(不与端点A,B重合),点E从点A出发沿x轴正方向以每秒2个单位长度的速度向点B运动,同时点F从点B出发沿线段BC方向以每秒1个单位长度的速度向点C运动(当点E停止时,点F也同时停止),当两个动点运动了t秒时,解答下列问题: