题目内容
1.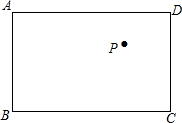 如图,在矩形ABCD中,AB=6,BC=8,P为矩形内一点,PE为点P到直线BC的距离,则PA+PD+PE的最小值为6+4$\sqrt{3}$.
如图,在矩形ABCD中,AB=6,BC=8,P为矩形内一点,PE为点P到直线BC的距离,则PA+PD+PE的最小值为6+4$\sqrt{3}$.
分析 如以AP、AE为边向左边作等边三角形△APN,△AEF,延长EP交AD于H,由△FAN≌△EAP,得到PE=FN,所以PA+PD+PE=PD+PN+FN,所以当F、N、P、D共线时,PA+PN+PD最短,分别求出DN、FN即可解决问题.
解答 解:如图 以AP、AE为边向左边作等边三角形△APN,△AEF,延长EP交AD于H,
以AP、AE为边向左边作等边三角形△APN,△AEF,延长EP交AD于H,
∵∠FAE=∠NAP,
∴∠FAN=∠EAP,
在△FAN和△EAP中,
$\left\{\begin{array}{l}{AF=AE}\\{∠FAN=∠EAP}\\{AN=AP}\end{array}\right.$,
∴△FAN≌△EAP,
∴PE=FN,
∴PA+PD+PE=PD+PN+FN,
∴当F、N、P、D共线时,PA+PN+PD最短,此时∠APD=∠ANF=∠APE=∠DPE=120°,∠PAD=∠PDA=30°,
在RT△ADN中,∵AD=8,∠ADN=30°,
∴AN=$\frac{8\sqrt{3}}{3}$,DN=$\frac{16\sqrt{3}}{3}$,PH=$\frac{1}{2}$AN=$\frac{4\sqrt{3}}{3}$,PE=6-$\frac{4\sqrt{3}}{3}$,
∴PA+PD+PE的最小值=DN+FN=DN+PE=$\frac{16\sqrt{3}}{3}$+6-$\frac{4\sqrt{3}}{3}$=6+4$\sqrt{3}$.
点评 本题考查矩形的性质、等边三角形的性质,解题关键添加辅助线构造全等三角形把线段PD、PA、PE拼在一起,共线时线段最短,题目难度比较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
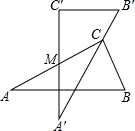 两块完全一样的含30°角的直角三角板,将它们重叠在一起并绕其较长直角边的中点M转动,使上面一块三角板的斜边刚好过下面一块三角板的直角顶点C,如图所示.已知AC=6,则这两块直角三角板顶点A、A′之间的距离等于3.
两块完全一样的含30°角的直角三角板,将它们重叠在一起并绕其较长直角边的中点M转动,使上面一块三角板的斜边刚好过下面一块三角板的直角顶点C,如图所示.已知AC=6,则这两块直角三角板顶点A、A′之间的距离等于3.
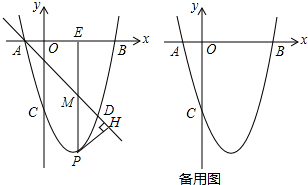
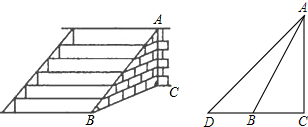
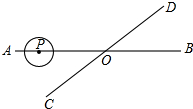 如图,直线AB,CD相交于点O,∠AOC=30°,半径为1cm的圆P的圆心在直线AB上,且与点O的距离为10cm,如果⊙P以2cm∕s的速度,沿由A向B的方向移动,那么4或6秒钟后⊙P与直线CD相切.
如图,直线AB,CD相交于点O,∠AOC=30°,半径为1cm的圆P的圆心在直线AB上,且与点O的距离为10cm,如果⊙P以2cm∕s的速度,沿由A向B的方向移动,那么4或6秒钟后⊙P与直线CD相切.