题目内容
抛物线y=2(x-2)2-6的顶点为C,已知y=-kx+2的图象经过点C,则这个一次函数图象与两坐标轴所围成的三角形面积为 .
考点:二次函数的性质
专题:
分析:根据抛物线解析式求出顶点坐标,然后代入一次函数解析式求出k值,再求出一次函数与坐标轴的交点,然后根据三角形的面积公式列式计算即可得解.
解答:解:抛物线y=2(x-2)2-6的顶点C(2,-6),
∵y=-kx+2的图象经过点C,
∴-2k+2=-6,
解得k=4,
∴y=4x+2,
令y=0,则4x+2=0,解得x=-
,
令x=0,则y=2,
所以,一次函数图象与两坐标轴所围成的三角形面积=
×2×
=
.
故答案为:
.
∵y=-kx+2的图象经过点C,
∴-2k+2=-6,
解得k=4,
∴y=4x+2,
令y=0,则4x+2=0,解得x=-
| 1 |
| 2 |
令x=0,则y=2,
所以,一次函数图象与两坐标轴所围成的三角形面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查了二次函数的性质,一次函数与坐标轴的交点坐标的求解,三角形的面积,是基础题,先求出二次函数顶点坐标是解题的关键.

练习册系列答案
相关题目
下列定理中有逆定理的是( )
| A、全等三角形对应角相等 |
| B、若a=0,则ab=0 |
| C、等腰三角形两腰上的高线相等 |
| D、负数的绝对值等于他的相反数 |
 如图,在平面直角坐标系中,已知Rt△AOB的两条直角边OA、OB分别在y轴和x轴上,并且OA、OB的长分别是方程x2-7x+12=0的两根(OA<OB),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O运动;同时,动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A运动,设点P、Q运动的时间为t秒.
如图,在平面直角坐标系中,已知Rt△AOB的两条直角边OA、OB分别在y轴和x轴上,并且OA、OB的长分别是方程x2-7x+12=0的两根(OA<OB),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O运动;同时,动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A运动,设点P、Q运动的时间为t秒. 画出△ABC绕边AB的中点O旋转180°后的图形.
画出△ABC绕边AB的中点O旋转180°后的图形.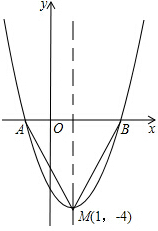 如图是二次函数y=x2+bx+c的图象,其顶点坐标为M(1,-4).
如图是二次函数y=x2+bx+c的图象,其顶点坐标为M(1,-4).