题目内容
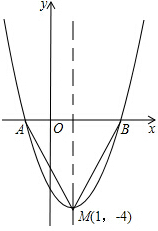 如图是二次函数y=x2+bx+c的图象,其顶点坐标为M(1,-4).
如图是二次函数y=x2+bx+c的图象,其顶点坐标为M(1,-4).(1)求出图象与x轴的交点A,B的坐标;
(2)在二次函数的图象上是否存在点P,使S△PAB=
| 5 |
| 4 |
考点:二次函数综合题
专题:压轴题
分析:(1)根据a=1设出抛物线顶点式解析式,然后令y=0解关于x的一元二次方程即可得到点A、B的坐标;
(2)求出△PAB的面积,再求出点P的纵坐标,然后代入抛物线解析式求解即可.
(2)求出△PAB的面积,再求出点P的纵坐标,然后代入抛物线解析式求解即可.
解答:解:(1)由已知得,抛物线解析式y=(x-1)2-4,
令y=0,则(x-1)2-4=0,
解得x1=-1,x2=3,
所以,点A(-1,0),B(3,0);
(2)∵A(-1,0),B(3,0),M(-1,-4),
∴AB=3-(-1)=3+1=4,点M到AB的距离为4,
∴S△MAB=
×4×4=8,
∵S△PAB=
S△MAB,
∴S△PAB=
×8=10,
∵AB=4,
∴yP=5,
令y=5,则(x-1)2-4=5,
解得x1=4,x2=-2,
∴点P(-2,5)或P(4,5).
令y=0,则(x-1)2-4=0,
解得x1=-1,x2=3,
所以,点A(-1,0),B(3,0);
(2)∵A(-1,0),B(3,0),M(-1,-4),
∴AB=3-(-1)=3+1=4,点M到AB的距离为4,
∴S△MAB=
| 1 |
| 2 |
∵S△PAB=
| 5 |
| 4 |
∴S△PAB=
| 5 |
| 4 |
∵AB=4,
∴yP=5,
令y=5,则(x-1)2-4=5,
解得x1=4,x2=-2,
∴点P(-2,5)或P(4,5).
点评:本题是二次函数综合题型,主要利用了抛物线与x轴的交点问题的求解,三角形的面积,二次函数图象上点的坐标特征,(1)写出顶点式解析式求解更简便,(2)难点在于先求出点P的纵坐标.

练习册系列答案
相关题目
关于x的一元二次方程x2-4x+5+m2=0的根的情况是( )
| A、有两个不相等的实数根 |
| B、有两个相等的实数根 |
| C、没有实数根 |
| D、根的情况不能确定 |
 如图,正方形网格中,△ABC为格点三角形(顶点都是格点),将△ABC绕点A按逆时针方向旋转90°得到△AB1C1(B与B1是对应点).请你在正方形网格中,作出△AB1C1.
如图,正方形网格中,△ABC为格点三角形(顶点都是格点),将△ABC绕点A按逆时针方向旋转90°得到△AB1C1(B与B1是对应点).请你在正方形网格中,作出△AB1C1. 如图,△ABC为等边三角形,边长为2,DE∥BC,△BCD的面积是△ABC面积的
如图,△ABC为等边三角形,边长为2,DE∥BC,△BCD的面积是△ABC面积的