Question

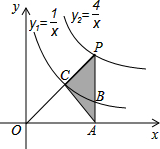如图，已知双曲线y₁=

1

x

（x＞0），y₂=

4

x

（x＞0），点P为双曲线y₂=

4

x

上的一点，且PA⊥x轴于点A，PA，PO分别交双曲线y₁=

1

x

于B，C两点，则△PAC的面积为（　　）

• A、1
• B、1.5
• C、2
• D、3

Answer 1

考点：反比例函数系数k的几何意义

专题：常规题型

分析：作CH⊥x轴于H，根据反比例函数y=

k

x

（k≠0）系数k的几何意义得到S_△OCH=

1

2

，S_△OPA=2，由CH∥PA，判断△OCH∽△OPA，利用相似的性质得到S_△OCH：S_△OPA=OH²：OA²=

1

2

：2，则OH：OA=1：2，所以S_△OCA=2S_△OCH=1，然后利用△PAC的面积=S_△OPA-S_△OCH进行计算．

解答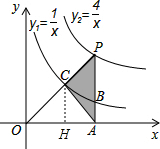：解：作CH⊥x轴于H，如图，
S_△OCH=

1

2

×1=

1

2

，S_△OPA=

1

2

×4=2，
∵CH∥PA，
∴△OCH∽△OPA，
∴S_△OCH：S_△OPA=OH²：OA²=

1

2

：2，
∴OH：OA=1：2，
∴S_△OCA=2S_△OCH=1，
∴△PAC的面积=S_△OPA-S_△OCH=1．
故选A．

点评：本题考查了反比例函数y=

k

x

（k≠0）系数k的几何意义：从反比例函数y=kx（k≠0）图象上任意一点向x轴和y轴作垂线，垂线与坐标轴所围成的矩形面积为|k|．