题目内容
 如图,PA,PB是⊙O的切线,点A,B为切点,AC是⊙O的直径,∠ACB=70°.则∠P的度数为
如图,PA,PB是⊙O的切线,点A,B为切点,AC是⊙O的直径,∠ACB=70°.则∠P的度数为考点:切线的性质
专题:
分析:根据PA,PB分别是⊙O的切线得到PA⊥OA,PB⊥OB,在四边形AOBP中根据内角和定理,就可以求出∠P的度数.
解答: 解:如图,连接OB.则∠AOB=2∠ACB,
解:如图,连接OB.则∠AOB=2∠ACB,
∵∠ACB=70°,
∴∠AOB=140°;
∵PA,PB分别是⊙O的切线,
∴PA⊥OA,PB⊥OB,
即∠PAO=∠PBO=90°,
∵四边形AOBP的内角和为360°,
∴∠P=360°-(90°+90°+140°)=40°.
故填:40°
 解:如图,连接OB.则∠AOB=2∠ACB,
解:如图,连接OB.则∠AOB=2∠ACB,∵∠ACB=70°,
∴∠AOB=140°;
∵PA,PB分别是⊙O的切线,
∴PA⊥OA,PB⊥OB,
即∠PAO=∠PBO=90°,
∵四边形AOBP的内角和为360°,
∴∠P=360°-(90°+90°+140°)=40°.
故填:40°
点评:本题主要考查了切线的性质,切线垂直于过切点的半径.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 如图,在平面直角坐标系中,一次函数y=-
如图,在平面直角坐标系中,一次函数y=-| 4 |
| 3 |
| k |
| x |
(1)k的值是
(2)点P在x轴上,且满足以点A、B、P为顶点的三角形是等腰三角形,则P点的坐标
 已知A是
已知A是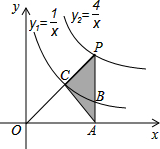 如图,已知双曲线y1=
如图,已知双曲线y1=