题目内容
 如图,点A,B,C,D为⊙O上的四个点,AC平分∠BAD,AC交BD于点E,CE=2,CD=3,则AE的长为( )
如图,点A,B,C,D为⊙O上的四个点,AC平分∠BAD,AC交BD于点E,CE=2,CD=3,则AE的长为( )| A、2 | B、2.5 | C、3 | D、3.5 |
考点:相似三角形的判定与性质,圆周角定理
专题:
分析:根据圆周角定理∠CAD=∠CDB,继而证明△ACD∽△DCE,设AE=x,则AC=x+2,利用对应边成比例,可求出x的值.
解答:解:设AE=x,则AC=x+2,
∵AC平分∠BAD,
∴∠BAC=∠CAD,
∵∠CDB=∠BAC(圆周角定理),
∴∠CAD=∠CDB,
∴△ACD∽△DCE,
∴
=
,
即
=
,
解得:x=2.5.
故选B.
∵AC平分∠BAD,
∴∠BAC=∠CAD,
∵∠CDB=∠BAC(圆周角定理),
∴∠CAD=∠CDB,
∴△ACD∽△DCE,
∴
| CD |
| CE |
| AC |
| DC |
即
| 3 |
| 2 |
| x+2 |
| 3 |
解得:x=2.5.
故选B.
点评:本题考查了圆周角定理、相似三角形的判定与性质,解答本题的关键是得出∠CAD=∠CDB,证明△ACD∽△DCE.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
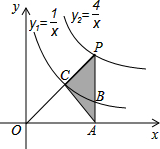 如图,已知双曲线y1=
如图,已知双曲线y1=| 1 |
| x |
| 4 |
| x |
| 4 |
| x |
| 1 |
| x |
| A、1 | B、1.5 | C、2 | D、3 |
下列美丽的图案中是轴对称图形的有( )


| A、4个 | B、3个 | C、2个 | D、1个 |
已知⊙O1、⊙O2的半径分别为3cm、8cm,且它们的圆心距为5cm,则⊙O1与⊙O2的位置关系是( )
| A、外切 | B、相交 | C、内切 | D、内含 |
 邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又余下一个四边形,称为第二次操作;…依此类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形.如图,?ABCD中,若AB=2,BC=1,则?ABCD为1阶准菱形.已知?ABCD是邻边长分别为1,a(a>1),且是3阶准菱形,则a的所有可能值为
邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又余下一个四边形,称为第二次操作;…依此类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形.如图,?ABCD中,若AB=2,BC=1,则?ABCD为1阶准菱形.已知?ABCD是邻边长分别为1,a(a>1),且是3阶准菱形,则a的所有可能值为