题目内容
4.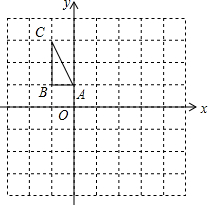 如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(0,1),B(-1,1),C(-1,3).
如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(0,1),B(-1,1),C(-1,3).(1)画出△ABC关于x轴对称的△A1B1C1;
(2)画出△ABC绕原点O顺时针方向旋转90°后得到的△A2B2C2;
(3)C1的坐标为(-1,-3),C2的坐标为(3,1),在(2)中点A旋转到A2经过的路径长为$\frac{1}{2}$π.
分析 (1)利用关于x轴对称的点的坐标特征,画出点A、B、C的对应点A1、B1、C1,即可得到△A1B1C1;
(2)利用网格特点和旋转的性质画出点A、B、C的对应点A2、B2、C2,即可得到△A2B2C2;
(3)利用所画图形写出C1和C2的坐标,(2)中点A旋转到A2经过的路径为以O为圆心,OA为半径的弧,于是可根据弧长公式计算点A旋转到A2经过的路径长.
解答  解:(1)如图,△A1B1C1为所作;
解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作;
(3)C1的坐标为(-1,-3),C2的坐标为(3,1),(2)中点A旋转到A2经过的路径长=$\frac{90•π•1}{180}$=$\frac{1}{2}$π.
故答案为(-1,-3 );(3,1 );$\frac{1}{2}$π.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了轴对称变换.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
17.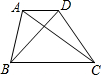 如图,在梯形ABCD中AD∥BC,对角线AC⊥BD,且AC=12,BD=9,则AD+BC=( )
如图,在梯形ABCD中AD∥BC,对角线AC⊥BD,且AC=12,BD=9,则AD+BC=( )
 如图,在梯形ABCD中AD∥BC,对角线AC⊥BD,且AC=12,BD=9,则AD+BC=( )
如图,在梯形ABCD中AD∥BC,对角线AC⊥BD,且AC=12,BD=9,则AD+BC=( )| A. | 20 | B. | 21 | C. | 15 | D. | 24 |
9.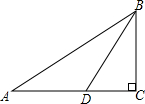 如图,在Rt△ABC中,∠C=90°,BD是角平分线,若CD=m,AB=n,则△ABD的面积是( )
如图,在Rt△ABC中,∠C=90°,BD是角平分线,若CD=m,AB=n,则△ABD的面积是( )
 如图,在Rt△ABC中,∠C=90°,BD是角平分线,若CD=m,AB=n,则△ABD的面积是( )
如图,在Rt△ABC中,∠C=90°,BD是角平分线,若CD=m,AB=n,则△ABD的面积是( )| A. | mn | B. | $\frac{1}{2}mn$ | C. | 2mn | D. | $\frac{1}{3}mn$ |
 如图,在△ABC中,AB=6cm,AC=5cm,∠ABC与∠ACB的平分线相交于点O,过点O作DE∥BC,分别交AB,AC于点D,E,则△ADE的周长=11cm.
如图,在△ABC中,AB=6cm,AC=5cm,∠ABC与∠ACB的平分线相交于点O,过点O作DE∥BC,分别交AB,AC于点D,E,则△ADE的周长=11cm. 在平面直角坐标系中,已知两点A(2,0)和M(1,-1),过点M作直线l⊥x轴,直线l上有两动点E和F(点F在点M的上方),且ME=MF.
在平面直角坐标系中,已知两点A(2,0)和M(1,-1),过点M作直线l⊥x轴,直线l上有两动点E和F(点F在点M的上方),且ME=MF.