题目内容
已知关于x的方程x2-2(m+1)x+m2-3=0
(1)若方程有实数根,求实数m的取值范围;
(2)若方程两实数根分别为x1、x2,且(x1+x2)2-4x1x2-12=0,求实数m的值.
(1)若方程有实数根,求实数m的取值范围;
(2)若方程两实数根分别为x1、x2,且(x1+x2)2-4x1x2-12=0,求实数m的值.
考点:根的判别式,根与系数的关系
专题:计算题
分析:(1)根据根的判别式的意义得到△=4(m+1)2-4(m2-3)≥0,然后解不等式即可;
(2)根据根与系数的关系得到x1+x2=2(m+1),x1x2=m2-3,利用(x1+x2)2-4x1x2-12=0得到4(m+1)2-4(m2-3)-12=0,解此方程得到m=-
,然后根据(1)中m的取值范围确定满足条件的m的值.
(2)根据根与系数的关系得到x1+x2=2(m+1),x1x2=m2-3,利用(x1+x2)2-4x1x2-12=0得到4(m+1)2-4(m2-3)-12=0,解此方程得到m=-
| 1 |
| 2 |
解答:解:(1)根据题意得△=4(m+1)2-4(m2-3)≥0,
解得m≥-2;
(2)根据题意得x1+x2=2(m+1),x1x2=m2-3,
而(x1+x2)2-4x1x2-12=0,
所以4(m+1)2-4(m2-3)-12=0,
解得m=-
,
而m≥-2,
所以m的值为-
.
解得m≥-2;
(2)根据题意得x1+x2=2(m+1),x1x2=m2-3,
而(x1+x2)2-4x1x2-12=0,
所以4(m+1)2-4(m2-3)-12=0,
解得m=-
| 1 |
| 2 |
而m≥-2,
所以m的值为-
| 1 |
| 2 |
点评:本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.也考查了根与系数的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
解方程2x+
=2-
,去分母,得( )
| x-1 |
| 3 |
| 3x-1 |
| 2 |
| A、12x+2(x-1)=12+3(3x-1) |
| B、12x+2(x-1)=12-3(3x-1) |
| C、12x-2(x-1)=12+3(3x-1) |
| D、12x-2(x-1)=12-3(3x-1) |
根据2010年第六次全国人口普查主要数据公报,贵州省常住人口约为4156万人,这一数据可以用科学记数法表示为( )
| A、4.156×107人 |
| B、4.156×106人 |
| C、4156×104人 |
| D、4.156×103人 |
 如图,矩形ABCD中,AB=4,AD=9,点M在BC上,且BM:MC=1:2,DE⊥AM于点E,求DE的长.
如图,矩形ABCD中,AB=4,AD=9,点M在BC上,且BM:MC=1:2,DE⊥AM于点E,求DE的长.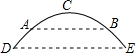 如图是某地一座抛物线形拱桥,桥拱在竖直平面内,与水面相交于A,B两点,拱桥最高点C到AB的距离为9m,AB=36m,D,E为拱桥底部的两点,且DE∥AB,点E到直线AB的距离为7m.建立平面直角坐标系,求:
如图是某地一座抛物线形拱桥,桥拱在竖直平面内,与水面相交于A,B两点,拱桥最高点C到AB的距离为9m,AB=36m,D,E为拱桥底部的两点,且DE∥AB,点E到直线AB的距离为7m.建立平面直角坐标系,求: