题目内容
11.若实数x、y满足$\sqrt{x+2}+{(y-\sqrt{5})^2}=0$,则xy的值是-2$\sqrt{5}$.分析 根据非负数的性质列式求出x、y的值,然后代入代数式进行计算即可得解.
解答 解:由题意得,x+2=0,y-$\sqrt{5}$=0,
解得x=-2,y=$\sqrt{5}$,
所以,xy=-2×$\sqrt{5}$=-2$\sqrt{5}$.
故答案为:-2$\sqrt{5}$.
点评 本题考查了非负数的性质:有限个非负数的和为零,那么每一个加数也必为零.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案
相关题目
2.函数y=$\frac{{{x^2}-6x}}{{{x^2}+2x+1}}$有( )
| A. | 最大值$\frac{9}{7}$ | B. | 最大值$-\frac{9}{7}$ | C. | 最小值$\frac{9}{7}$ | D. | 最小值$-\frac{9}{7}$ |
19.若某数的平方根为2a+3和a-15,则这个数是( )
| A. | -18 | B. | $-\frac{2}{3}$ | C. | 121 | D. | 以上结论都不是 |
20.已知数据:10,8,6,10,8,13,11,10,12,7,9,8,12,9,11,12,9,10,11,10,那么频数为4的一组是( )
| A. | 5.5~7.5 | B. | 7.5~9.5 | C. | 9.5~11.5 | D. | 11.5~13.5 |
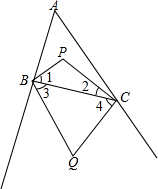 如图,在△ABC中,P是△ABC内角平分线的BP,CP的交点.Q是△ABC中∠B、∠C外角平分线的交点.
如图,在△ABC中,P是△ABC内角平分线的BP,CP的交点.Q是△ABC中∠B、∠C外角平分线的交点.