题目内容
6.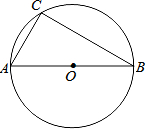 如图,⊙O的直径AB为10,弦AC为6.
如图,⊙O的直径AB为10,弦AC为6.(1)利用尺规作∠ACB的平分线CD,交⊙O于点D,连接AD、BD(保留作图痕迹,不写作法);
(2)在(1)所作的图形中,求AD与BD的长;
(3)求△ACD的面积.
分析 (1)作DC平分∠ACB交⊙O于D;
(2)根据圆周角定理,由AB为直径得到∠ADB=90°,由∠DCA=∠DCB得$\widehat{DA}$=$\widehat{DB}$,则DA=DB,所以△ADB为等腰直角三角形,然后根据等腰直角三角形的性质计算DA和DB;
(3)作AH⊥CD于H,如图,先得到∠ACH=45°,根据等腰直角三角形的性质得HC=HA=$\frac{\sqrt{2}}{2}$AC=3$\sqrt{2}$,在Rt△ADH中,利用勾股定理计算出DH=4$\sqrt{2}$,则CD=CH+DH=7$\sqrt{2}$,然后根据三角形面积公式求解.
解答 解:(1)如图,CD、AD、BD为所作;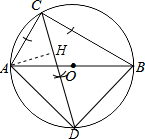
(2)∵AB为直径,
∴∠ADB=90°,
∵CD平分∠ACB,
∴∠DCA=∠DCB,
∴$\widehat{DA}$=$\widehat{DB}$,
∴DA=DB,
∴△ADB为等腰直角三角形,
∴AD=BD=$\frac{\sqrt{2}}{2}$AB=$\frac{\sqrt{2}}{2}$×10=5$\sqrt{2}$;
(3)作AH⊥CD于H,如图,
∵AB为直径,
∴∠ACB=90°,
∴∠ACH=45°,
∴HC=HA=$\frac{\sqrt{2}}{2}$AC=3$\sqrt{2}$,
在Rt△ADH中,DH=$\sqrt{A{D}^{2}-A{H}^{2}}$=$\sqrt{(5\sqrt{2})^{2}-(3\sqrt{2})^{2}}$=4$\sqrt{2}$,
∴CD=CH+DH=7$\sqrt{2}$,
∴S△ACD=$\frac{1}{2}$•AH•CD=$\frac{1}{2}$×3$\sqrt{2}$×7$\sqrt{2}$=21.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了圆周角定理和勾股定理.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| 第1列 | 第2列 | 第3列 | … | 第n列 | |
| 第1行 | 1 | 2 | 3 | … | n |
| 第2行 | n+1 | n+2 | n+3 | … | 2n |
| 第3行 | 2n+1 | 2n+2 | 2n+3 | … | 3n |
| … | … | … | … | … | … |
| A. | 平行四边形 | B. | 菱形 | C. | 矩形 | D. | 等边三角形 |
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
 如图,P为菱形ABCD的对角线上一点,PE丄AB于点E,PF丄AD于点F,PF=6
如图,P为菱形ABCD的对角线上一点,PE丄AB于点E,PF丄AD于点F,PF=6 如图,已知∠AOB等于30°,角内有一点P,OP=6,点M在OA上,点N在OB上,△PMN周长的最小值是6.
如图,已知∠AOB等于30°,角内有一点P,OP=6,点M在OA上,点N在OB上,△PMN周长的最小值是6.