题目内容
18. 如图,在△ABC中,高BD,CE相交于点H,若∠BHC=110°,则∠A等于70°.
如图,在△ABC中,高BD,CE相交于点H,若∠BHC=110°,则∠A等于70°.
分析 先根据垂直的定义得出∠BEH=∠HDC=90°,由三角形外角的性质得出∠EBH与∠DCH的度数,再根据三角形内角和定理求出∠HBC+∠HCB的度数,进而可得出∠ABC+∠ACB的度数,由此可得出结论.
解答 解:∵BD⊥AC,CE⊥AB,
∴∠BEH=∠HDC=90°.
∵∠BHC=110°,
∴∠EBH=∠DCH=110°-90°=20°,∠HBC+∠HCB=180°-110°=70°,
∴∠ABC+∠ACB=∠EBH+∠DCH+(∠HBC+∠HCB)=20°+20°+70°=110°,
∴∠A=180°-110°=70°.
故答案为:70°.
点评 本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.一种零件规定直径为200mm,为检测它们的直径大小,从中抽取6件进行检测,比规定直径大的毫米数记作正数,比规定直径小的毫米数记作负数,检测记录如下:(单位:mm)
几号零件的直径最大?几号零件的直径最小?并求出最大直径和最小直径.
| 1号零件 | 2号零件 | 3号零件 | 4号零件 | 5号零件 | 6号零件 |
| 0.2 | -0.1 | -0.3 | 0.1 | 0 | -0.2 |
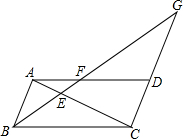 如图,在平行四边形ABCD中,点G在CD的延长线上,连接BG分别交AC、AD于E、F,求证:BE、BF、BG之间满足的数量关系.
如图,在平行四边形ABCD中,点G在CD的延长线上,连接BG分别交AC、AD于E、F,求证:BE、BF、BG之间满足的数量关系.