题目内容
2.设a,b是不小于3的实数,则$\sqrt{a-2}$+|2-$\sqrt{b-2}$|的最小值是1.分析 根据a,b是不小于3的实数,可得当a=3时,$\sqrt{a-2}$的最小值为1,当b=6时,|2-$\sqrt{b-2}$|的最小值是0,据此可得$\sqrt{a-2}$+|2-$\sqrt{b-2}$|的最小值.
解答 解:∵a,b是不小于3的实数,
∴当a=3时,$\sqrt{a-2}$的最小值为1,
当b=6时,|2-$\sqrt{b-2}$|的最小值是0,
∴$\sqrt{a-2}$+|2-$\sqrt{b-2}$|的最小值=1+0=1,
故答案为:1.
点评 此题考查了非负数的性质的运用.解此题的关键是由a,b均为不小于3的实数,求得$\sqrt{a-2}$≥1,|2-$\sqrt{b-2}$|≥0.

练习册系列答案
相关题目
17.如果△ABC三边a、b、c满足(a-4)2+$\sqrt{b-3}$+|c-5|=0,那么△ABC的形状是( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 等腰三角形 | D. | 直角三角形 |
7.研究表明,某种动物体内的一种细胞直径约为0.000 00156m,用科学记数法表示是( )
| A. | 1.56×10-7 m | B. | 1.56×10-6m | C. | 1.56×10-8 m | D. | 1.56×10-9 m |
14.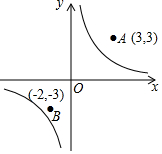 反比例函数的图象如图所示,则这个反比例函数的解析式可能是( )
反比例函数的图象如图所示,则这个反比例函数的解析式可能是( )
 反比例函数的图象如图所示,则这个反比例函数的解析式可能是( )
反比例函数的图象如图所示,则这个反比例函数的解析式可能是( )| A. | y=$\frac{2}{x}$ | B. | y=$\frac{6}{x}$ | C. | y=$\frac{7}{x}$ | D. | y=$\frac{9}{x}$ |
12.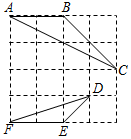 在4×4的正方形网格中,△ABC和△DEF的顶点都在边长为1的正方形的顶点上,则图中∠ACB的正切值为( )
在4×4的正方形网格中,△ABC和△DEF的顶点都在边长为1的正方形的顶点上,则图中∠ACB的正切值为( )
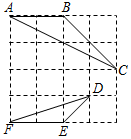 在4×4的正方形网格中,△ABC和△DEF的顶点都在边长为1的正方形的顶点上,则图中∠ACB的正切值为( )
在4×4的正方形网格中,△ABC和△DEF的顶点都在边长为1的正方形的顶点上,则图中∠ACB的正切值为( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 3 |
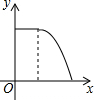
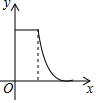
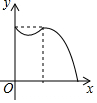
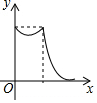
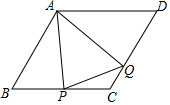 如图,在菱形ABCD中,点P从点B匀速出发,沿着B→C→D方向运动至点D停止;同时点Q从点C匀速出发,沿着C→D→A方向运动至点A停止;点P,Q运动速度相同,则△APQ的面积y与点P运动的路程x之间形成的函数关系的图象大致是( )
如图,在菱形ABCD中,点P从点B匀速出发,沿着B→C→D方向运动至点D停止;同时点Q从点C匀速出发,沿着C→D→A方向运动至点A停止;点P,Q运动速度相同,则△APQ的面积y与点P运动的路程x之间形成的函数关系的图象大致是( )