题目内容
12.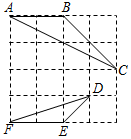 在4×4的正方形网格中,△ABC和△DEF的顶点都在边长为1的正方形的顶点上,则图中∠ACB的正切值为( )
在4×4的正方形网格中,△ABC和△DEF的顶点都在边长为1的正方形的顶点上,则图中∠ACB的正切值为( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 3 |
分析 根据勾股定理即可求出AC、BC、DE、DF的长度,然后证明△FDE∽△ABC,推出∠ACB=∠DFE,由此即可解决问题.
解答 解:由勾股定理 可求出:BC=2$\sqrt{2}$,AC=2$\sqrt{5}$,DF=$\sqrt{10}$,DE=$\sqrt{2}$,
∴$\frac{FD}{AC}$=$\frac{\sqrt{2}}{2}$$\frac{FE}{BC}$=$\frac{\sqrt{2}}{2}$,$\frac{ED}{AB}$=$\frac{\sqrt{2}}{2}$,
∴$\frac{FD}{AC}$=$\frac{ED}{AB}$=$\frac{EF}{BC}$,
∴△FDE∽△CAB,
∴∠DFE=∠ACB,
∴tan∠DFE=tan∠ACB=$\frac{1}{3}$,
故选(B)
点评 本题考查解直角三角形,涉及勾股定理,相似三角形的判定与性质,解题的关键是灵活运用相似三角形的性质解决问题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
3.点P(2,-3)关于x轴的对称点的坐标为( )
| A. | (-2,-3) | B. | (2,3) | C. | (-2,3) | D. | (3,-2) |
20.2015年双11淘宝全天交易额约为921亿,将数字921亿用科学记数法表示为( )
| A. | 9.21×108 | B. | 9.21×1010 | C. | 92.1×109 | D. | 921×108 |
7.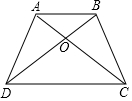 如图所示,四边形ABCD的两条对角线交于点O,且AB∥CD,下列结论中总能成立的有( )
如图所示,四边形ABCD的两条对角线交于点O,且AB∥CD,下列结论中总能成立的有( )
①△AOB与△COD相似;②△ABD与△ABC相似;
③S△DOC:S△AOB=DC:AB;④S△AOD=S△BOC.
 如图所示,四边形ABCD的两条对角线交于点O,且AB∥CD,下列结论中总能成立的有( )
如图所示,四边形ABCD的两条对角线交于点O,且AB∥CD,下列结论中总能成立的有( )①△AOB与△COD相似;②△ABD与△ABC相似;
③S△DOC:S△AOB=DC:AB;④S△AOD=S△BOC.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.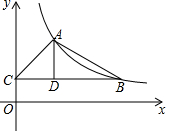 如图,在△ABC中,BC∥x轴,AD⊥BC,A,B两点恰好在反比例函数y=$\frac{k}{x}$(k>0)第一象限的图象上,若S△ACD=6,S△ABD=9,则k为( )
如图,在△ABC中,BC∥x轴,AD⊥BC,A,B两点恰好在反比例函数y=$\frac{k}{x}$(k>0)第一象限的图象上,若S△ACD=6,S△ABD=9,则k为( )
 如图,在△ABC中,BC∥x轴,AD⊥BC,A,B两点恰好在反比例函数y=$\frac{k}{x}$(k>0)第一象限的图象上,若S△ACD=6,S△ABD=9,则k为( )
如图,在△ABC中,BC∥x轴,AD⊥BC,A,B两点恰好在反比例函数y=$\frac{k}{x}$(k>0)第一象限的图象上,若S△ACD=6,S△ABD=9,则k为( )| A. | 10 | B. | 15 | C. | 18 | D. | 20 |
4. 三国魏景元四年(公元263年),由我国古典数学理论的奠基人之一刘徽完成了《九章算术注》十卷,《重差》为第一卷,它是我国学者编撰的最早的一部测量数学著作,亦为地图学提供了数学基础,该卷中的第一个问题是求海岛上的山峰的高度,这本书的名称是( )
三国魏景元四年(公元263年),由我国古典数学理论的奠基人之一刘徽完成了《九章算术注》十卷,《重差》为第一卷,它是我国学者编撰的最早的一部测量数学著作,亦为地图学提供了数学基础,该卷中的第一个问题是求海岛上的山峰的高度,这本书的名称是( )
 三国魏景元四年(公元263年),由我国古典数学理论的奠基人之一刘徽完成了《九章算术注》十卷,《重差》为第一卷,它是我国学者编撰的最早的一部测量数学著作,亦为地图学提供了数学基础,该卷中的第一个问题是求海岛上的山峰的高度,这本书的名称是( )
三国魏景元四年(公元263年),由我国古典数学理论的奠基人之一刘徽完成了《九章算术注》十卷,《重差》为第一卷,它是我国学者编撰的最早的一部测量数学著作,亦为地图学提供了数学基础,该卷中的第一个问题是求海岛上的山峰的高度,这本书的名称是( )| A. | 《海岛算经》 | B. | 《孙子算经》 | C. | 《九章算术》 | D. | 《五经算术》 |
1.a的绝对值是( )
| A. | -a | B. | $\sqrt{a}$ | C. | |a| | D. | $\frac{1}{a}$ |
2.下面四个图案依次是我国汉字中的“福禄寿喜”的艺术字图.这四个图案中是中心对称图形的是( )


| A. | ①② | B. | ②③ | C. | ②④ | D. | ②③④ |