��Ŀ����
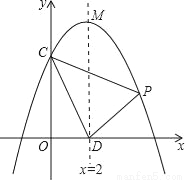
��ͼ��������y=ax2+bx+c��y���ڵ�C��0��4�����Գ���x=2��x�ύ�ڵ�D������ΪM����DM=OC+OD��
��1���������ߵĽ���ʽ��
��2�����P��x��y���ǵ�һ�����ڸ��������ϵ�һ�����㣬��PCD�����ΪS����S����x�ĺ�����ϵʽ��д���Ա���x��ȡֵ��Χ������xȡ����ʱ��S��ֵ�������Ƕ��٣�
��ϰ��ϵ�д�
�����Ŀ


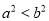 ����
����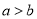 ������������
������������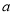 ��
�� 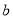 ��ֵ�У���˵����������Ǽ�������ǣ� ����
��ֵ�У���˵����������Ǽ�������ǣ� ����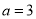 ��
�� 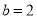 B.
B. 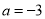 ��
�� 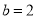 C.
C. 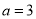 ��
�� 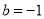 D.
D. 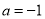 ��
�� 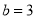
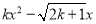 +1=0����������ȵ�ʵ��������ôk��ȡֵ��Χ�ǣ�������
+1=0����������ȵ�ʵ��������ôk��ȡֵ��Χ�ǣ�������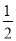 ��k��
��k��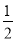 ��k��0 B. k��
��k��0 B. k��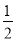 ��k��0
��k��0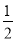 ��k��
��k��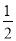 D. k��
D. k��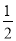
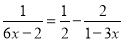
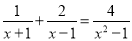 ��
��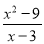 ��_____ʱ��ʽ��ֵΪ�㣬��_____ʱ����ʽ
��_____ʱ��ʽ��ֵΪ�㣬��_____ʱ����ʽ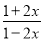 �����壮
�����壮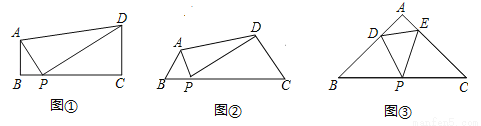
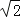 ��CE=3����DE�ij�������
��CE=3����DE�ij�������