题目内容
2.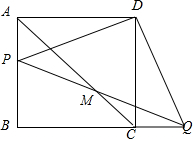 如图,在正方形ABCD中,AB=2,点P为边AB上一点.将△ADP旋转到△CDQ的位置上.连接AC,PQ交于点M,则$\sqrt{2}$AM-AP的值为2.
如图,在正方形ABCD中,AB=2,点P为边AB上一点.将△ADP旋转到△CDQ的位置上.连接AC,PQ交于点M,则$\sqrt{2}$AM-AP的值为2.
分析 先连接DM,过M作ME⊥AC交AD的延长线于E,过P作PF⊥AB交AC于F,根据△AEM和△APF都是等腰直角三角形,即可得到AP=FP,AM=EM,∠E=∠PAM=45°,AE=$\sqrt{2}$AM,根据旋转可得,AP=CQ,∠DCQ=∠DAP=90°,进而判定△FPM≌△CQM,得出M是PQ的中点,进而得到EM⊥AC,再判定△AMP≌△EMD,可得AP=DE,最后根据AE-DE=AD=2,即可得出$\sqrt{2}$AM-AP=2,
解答  解:如图所示,连接DM,过M作ME⊥AC交AD的延长线于E,过P作PF⊥AB交AC于F,则PF∥BC,
解:如图所示,连接DM,过M作ME⊥AC交AD的延长线于E,过P作PF⊥AB交AC于F,则PF∥BC,
∵∠PAF=∠DAM=45°,
∴△AEM和△APF都是等腰直角三角形,
∴AP=FP,AM=EM,∠E=∠PAM=45°,AE=$\sqrt{2}$AM,
由旋转可得,AP=CQ,∠DCQ=∠DAP=90°,
∴PF=QC,且B,C,Q在同一直线上,
∴CQ∥PF,
∴∠FPM=∠CQM,
在△FPM和△CQM中,
$\left\{\begin{array}{l}{∠FPM=∠CQM}\\{∠PMF=∠QMC}\\{PF=QC}\end{array}\right.$,
∴△FPM≌△CQM(AAS),
∴PM=QM,即M是PQ的中点,
由旋转可得,DP=DQ,
∴DM⊥PQ,
又∵EM⊥AC,
∴∠AMP=∠EMD,
在△AMP和△EMD中,
$\left\{\begin{array}{l}{∠AMP=∠EMD}\\{AM=EM}\\{∠PAM=∠E}\end{array}\right.$,
∴△AMP≌△EMD(ASA),
∴AP=DE,
∵AE-DE=AD=2,
∴$\sqrt{2}$AM-AP=2,
故答案为:2.
点评 本题主要考查了旋转的性质,正方形的性质以及等腰直角三角形的性质的综合应用,解决问题的关键是作辅助线构造等腰直角三角形以及全等三角形,依据全等三角形的对应边相等进行求解.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案| A. | 相等的角是对顶角 | |
| B. | 两条直线被第三条直线所截,同位角相等 | |
| C. | 任何数的偶次幂都大于0 | |
| D. | 在同一平面内,垂直于同一条直线的两条直线平行 |
| A. | 三角形 | B. | 长方形 | C. | 五边形 | D. | 六边形 |
 图中,AB=AC及AP平分∠BAC.AP是否为△ABC的一条垂直平分线?试解释你的答案.
图中,AB=AC及AP平分∠BAC.AP是否为△ABC的一条垂直平分线?试解释你的答案. 如图,CD⊥AB,点E、F在AB上,且CE=10cm,CD=8cm,CF=12cm,则点C到AB的距离是8cm.
如图,CD⊥AB,点E、F在AB上,且CE=10cm,CD=8cm,CF=12cm,则点C到AB的距离是8cm. 如图,已知OA⊥OB,OC⊥OD,且∠AOD:∠BOC=4:5,求∠BOC的度数.
如图,已知OA⊥OB,OC⊥OD,且∠AOD:∠BOC=4:5,求∠BOC的度数.