题目内容
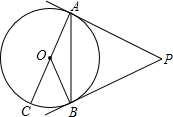 如图,PA,PB是⊙O是切线,A,B为切点,AC是⊙O的直径,若∠P=46°,求∠BAC的度数.
如图,PA,PB是⊙O是切线,A,B为切点,AC是⊙O的直径,若∠P=46°,求∠BAC的度数.考点:切线的性质
专题:
分析:根据切线的性质求出∠PAO的度数,进而求出∠BAC的度数问题即可解决.
解答: 解:∵PA,PB是⊙O是切线,
解:∵PA,PB是⊙O是切线,
∴PA=PB,又∠P=46°,
∴∠PAB=∠PBA=
=67°;
又∵PA是⊙O是切线,AO为半径,
∴OA⊥AP,
∴∠OAP=90°,
∴∠BAC=∠OAP-∠PAB=90°-67°=23°.
 解:∵PA,PB是⊙O是切线,
解:∵PA,PB是⊙O是切线,∴PA=PB,又∠P=46°,
∴∠PAB=∠PBA=
| 180°-46° |
| 2 |
又∵PA是⊙O是切线,AO为半径,
∴OA⊥AP,
∴∠OAP=90°,
∴∠BAC=∠OAP-∠PAB=90°-67°=23°.
点评:该题以园为载体,以切线的考查为核心构造而成;解题的关键是灵活运用有关定理来分析、解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图是抛物线y=ax2+bx+c(a≠0)的图象的一部分,已知抛物线的对称轴为x=2,与x轴的一个交点是(-1,0),下列结论其中正确的是( )
如图是抛物线y=ax2+bx+c(a≠0)的图象的一部分,已知抛物线的对称轴为x=2,与x轴的一个交点是(-1,0),下列结论其中正确的是( )| A、abc<0 |
| B、抛物线与x轴的另一个交点是(4,0) |
| C、12a+c>0 |
| D、点(-3,y1)、(6,y2)都在抛物线上,则有y1<y2 |
二次函数y=-2(x+1)2+2的图象大致是( )
A、 |
B、 |
C、 |
D、 |
在数轴上表示-12的点与表示4的点的距离是( )
| A、8 | B、-16 | C、16 | D、-8 |
 如图,△ABC中,AB=AC,AD∥BC.
如图,△ABC中,AB=AC,AD∥BC.