题目内容
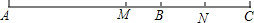 如图所示,已知线段AB=8cm,BC=3cm,点M、N分别是线段AC、BC的中点,求线段MN的长度;若线段BC为任意长度,其他条件不变,则线段M你的长度是否发生变化?请说明理由.
如图所示,已知线段AB=8cm,BC=3cm,点M、N分别是线段AC、BC的中点,求线段MN的长度;若线段BC为任意长度,其他条件不变,则线段M你的长度是否发生变化?请说明理由.考点:两点间的距离
专题:
分析:先根据线段AB=8cm,BC=3cm,点MN分别是线段AC、BC的中点求出MB,NB的长度,根据MN=MB+NB即可得出结论.
解答:解:∵线段AB=8cm,BC=3cm,点M,N分别是线段AC、BC的中点,
∴CM=
AC=
cm,NC=
BC=
cm,
∴MN=CM-NC=
-
=4(cm).
若线段BC为任意长度,其他条件不变,则线段MN的长度不变.
理由:∵点M,N分别是线段AC、BC的中点,
∴CM=
AC,NC=
BC
∴MN=CM-NC=
(AC-BC)=
AB.
∴CM=
| 1 |
| 2 |
| 11 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴MN=CM-NC=
| 11 |
| 2 |
| 3 |
| 2 |
若线段BC为任意长度,其他条件不变,则线段MN的长度不变.
理由:∵点M,N分别是线段AC、BC的中点,
∴CM=
| 1 |
| 2 |
| 1 |
| 2 |
∴MN=CM-NC=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查的是两点间的距离,熟知各线段之间的和、差及倍数关系是解答此题的关键.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
用一个平面去截四棱柱,截面形状不可能是( )
| A、三角形 | B、四边形 |
| C、六边形 | D、七边形 |
下列说法中,正确的是( )
| A、分数包括正分数、零、负分数 |
| B、正整数集合与负整数集合合在一起就构成整数集合 |
| C、整数和分数统称为有理数 |
| D、正数、负数和零统称为有理数 |
 如图,已知CE⊥AB,DF⊥AB,AC=BD,CE=DF,求证:AC∥BD.
如图,已知CE⊥AB,DF⊥AB,AC=BD,CE=DF,求证:AC∥BD.
 如图,△ABC中,AB=AC,AD∥BC.
如图,△ABC中,AB=AC,AD∥BC.