题目内容
已知梯形的两对角线之比为3:4,和为35,高为12,则梯形面积为 .
考点:梯形,勾股定理
专题:
分析:根据题意作图,分别利用勾股定理求得BF,CE的长,从而可得到上下底的和,根据梯形的面积公式计算即可.
解答: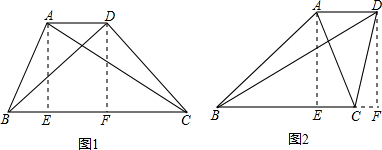 解:如图,梯形ABCD中,AD∥BC,AC:BD=3:4,AC+BD=35,DH=12,
解:如图,梯形ABCD中,AD∥BC,AC:BD=3:4,AC+BD=35,DH=12,
∴AC=15,BD=20,
解:作梯形的高AE,DF,如图1,
在直角三角形BDF中,利用勾股定理可求出BF=
=9,
在直角三角形ACE中,利用勾股定理可求出CE=
=16,
∴CE+BF=25=BC+EF
∵EF=AD
∴BC+AD=25
∴梯形的面积=25×12÷2=150.
②作梯形的高AE,DF,F在BC的延长线上,如图2:
在直角三角形BDF中,利用勾股定理可求出BF=
=
=16,
在直角三角形ACE中,利用勾股定理可求出CE=
=
=9,
∴AD+BC=BC+EF=BF+EC=25,
∴梯形的面积=
(AD+BC)×AE=
(BF-EC)×AE=
×25×12=150.
综上所述,梯形的面积是150.
故答案是:150.
 解:如图,梯形ABCD中,AD∥BC,AC:BD=3:4,AC+BD=35,DH=12,
解:如图,梯形ABCD中,AD∥BC,AC:BD=3:4,AC+BD=35,DH=12,∴AC=15,BD=20,
解:作梯形的高AE,DF,如图1,
在直角三角形BDF中,利用勾股定理可求出BF=
| 152-122 |
在直角三角形ACE中,利用勾股定理可求出CE=
| 202-122 |
∴CE+BF=25=BC+EF
∵EF=AD
∴BC+AD=25
∴梯形的面积=25×12÷2=150.
②作梯形的高AE,DF,F在BC的延长线上,如图2:
在直角三角形BDF中,利用勾股定理可求出BF=
| BD2-DF2 |
| 202-122 |
在直角三角形ACE中,利用勾股定理可求出CE=
| AC2-AE2 |
| 152-122 |
∴AD+BC=BC+EF=BF+EC=25,
∴梯形的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
综上所述,梯形的面积是150.
故答案是:150.
点评:考查了梯形,本题的基本公式是梯形的面积,但要求梯形的面积就要有上底和下底的长,所以此题的关键之外是利用勾股定理求出上底和下底的长.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
△ABC中,A、B两点坐标分别是(0,0)和(36,15),点C的横、纵坐标均为整数,则△ABC的面积的最小值是( )
A、
| ||
| B、1 | ||
C、
| ||
| D、不存在最小值 |
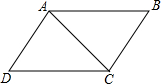 如图,已知△ABC≌△CDA,A和C,D和B分别是对应点,如果AB=7cm,AD=
如图,已知△ABC≌△CDA,A和C,D和B分别是对应点,如果AB=7cm,AD=6cm,AC=4cm,则DC的长为( )
| A、6cm | B、7cm |
| C、4cm | D、不确定 |
在-
,
,
4.
,
,
,这几个数中无理数有( )个.
| 22 |
| 7 |
| 3 | 9 |
| 25 |
| • |
| 2 |
| π |
| 2 |
| 0.4 |
| A、4 | B、3 | C、2 | D、1 |
 如图,矩形ABCD中,AB=3cm,AD=9cm,过对角线BD的中点O作BD的垂直平分线EF分别交AD,BC于E,F,则EF长为
如图,矩形ABCD中,AB=3cm,AD=9cm,过对角线BD的中点O作BD的垂直平分线EF分别交AD,BC于E,F,则EF长为