题目内容
 如图,矩形ABCD中,AB=3cm,AD=9cm,过对角线BD的中点O作BD的垂直平分线EF分别交AD,BC于E,F,则EF长为
如图,矩形ABCD中,AB=3cm,AD=9cm,过对角线BD的中点O作BD的垂直平分线EF分别交AD,BC于E,F,则EF长为考点:矩形的性质,线段垂直平分线的性质,勾股定理
专题:
分析:连接EB,构造直角三角形,设AE为x,则DE=BE=4-x,利用勾股定理得到有关x的一元一次方程,求得x,即可求出BE的长.
解答:解:连接EB,
∵EF垂直平分BD,
∴ED=EB,
设AE=xcm,则DE=EB=(9-x)cm,
在Rt△AEB中,
AE2+AB2=BE2,
即:x2+32=(9-x)2,
解得:x=4,
则BE=9-4=5(cm),
∵矩形ABCD中,AB=3cm,AD=9cm,
∴BD=
=3
(cm),
则BO=
cm,
故EO=
=
(cm),
则EF=
cm.
故答案为:
cm.
∵EF垂直平分BD,

∴ED=EB,
设AE=xcm,则DE=EB=(9-x)cm,
在Rt△AEB中,
AE2+AB2=BE2,
即:x2+32=(9-x)2,
解得:x=4,
则BE=9-4=5(cm),
∵矩形ABCD中,AB=3cm,AD=9cm,
∴BD=
| 92+32 |
| 10 |
则BO=
3
| ||
| 2 |
故EO=
| BE2-BO2 |
| ||
| 2 |
则EF=
| 10 |
故答案为:
| 10 |
点评:本题考查了勾股定理的内容,利用勾股定理不单单能在直角三角形中求边长,而且能利用勾股定理这一隐含的等量关系列出方程.

练习册系列答案
相关题目
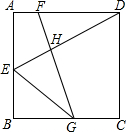 如图,在正方形ABCD中,点E是AB上一点,G是BC上一点,FG⊥DE交于点H,FG=DE,求证:FD+EG≥
如图,在正方形ABCD中,点E是AB上一点,G是BC上一点,FG⊥DE交于点H,FG=DE,求证:FD+EG≥ 如图,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交AB于E,交⊙O于D.求弦CB、AD的长.
如图,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交AB于E,交⊙O于D.求弦CB、AD的长.