题目内容
△ABC中,A、B两点坐标分别是(0,0)和(36,15),点C的横、纵坐标均为整数,则△ABC的面积的最小值是( )
A、
| ||
| B、1 | ||
C、
| ||
| D、不存在最小值 |
考点:面积及等积变换,相似三角形的判定与性质
专题:
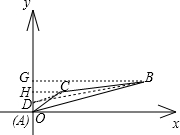
分析:过点C作CH⊥y轴于H,过点B作BG⊥y轴于G,过点C作CD∥AB,交y轴于点D,设点C的坐标为(x,y),其中x、y均为整数,根据等积变换可得S△CAB=S△DAB=18AD.易证△DHC∽△AGB,利用相似三角形的性质可得到DH=
x,进而可得到S△CAB=
,由x、y是整数及S△CAB>0可得到12y-5x是正整数,则有12y-5x≥1,从而可求出△ABC的面积的最小值.
| 5 |
| 12 |
| 3(12y-5x) |
| 2 |
解答:解:过点C作CH⊥y轴于H,过点B作BG⊥y轴于G,过点C作CD∥AB,交y轴于点D,
设点C的坐标为(x,y),其中x、y均为整数,如图,
则有CH=x,AH=OH=y,S△CAB=S△DAB=
AD•BG=
×AD×36=18AD,
∠CDH=∠BAG,∠DHC=∠AGB=90°,
∴△DHC∽△AGB,
∴
=
.
∵AG=15,BG=36,CH=x,
∴DH=
x=
x,
∴AD=AH-DH=y-
x,
∴S△CAB=18(y-
x)
=18y-
x=
=
.
∵x、y是整数,
∴12y-5x也是整数.
∵S△CAB>0,
∴12y-5x是正整数,
∴12y-5x≥1,
∴S△CAB≥
.
当y=3,x=7时,S△CAB取到最小值,最小值为
.
故选:C.
设点C的坐标为(x,y),其中x、y均为整数,如图,
则有CH=x,AH=OH=y,S△CAB=S△DAB=
| 1 |
| 2 |
| 1 |
| 2 |
∠CDH=∠BAG,∠DHC=∠AGB=90°,
∴△DHC∽△AGB,
∴
| DH |
| AG |
| CH |
| BG |

∵AG=15,BG=36,CH=x,
∴DH=
| 15 |
| 36 |
| 5 |
| 12 |
∴AD=AH-DH=y-
| 5 |
| 12 |
∴S△CAB=18(y-
| 5 |
| 12 |
=18y-
| 15 |
| 2 |
| 36y-15x |
| 2 |
| 3(12y-5x) |
| 2 |
∵x、y是整数,
∴12y-5x也是整数.
∵S△CAB>0,
∴12y-5x是正整数,
∴12y-5x≥1,
∴S△CAB≥
| 3 |
| 2 |
当y=3,x=7时,S△CAB取到最小值,最小值为
| 3 |
| 2 |
故选:C.
点评:本题主要考查了相似三角形的判定与性质、等积变换等知识,有一定的难度.而运用等积变换将△CAB的面积转化为△DAB的面积则是解决本题的关键.

练习册系列答案
相关题目
下列图形中不是中心对称的图形是( )
| A、矩形 | B、菱形 |
| C、正方形 | D、等腰梯形 |
 如图,已知矩形ABCD,AB=2,AD=4,点P在BC上移动,△ABP和△PCD能相似吗?若能,求出点P的位置;若不能,请说明理由.
如图,已知矩形ABCD,AB=2,AD=4,点P在BC上移动,△ABP和△PCD能相似吗?若能,求出点P的位置;若不能,请说明理由.