题目内容
已知
+
=
，其中，a＞0，请就正数a的取值，讨论方程解的情况．
x+
|
x-
|
| a |
考点：二次根式的化简求值
专题：计算题
分析：先把已知条件两边平方后整理得到|x-1|+2x=a，分类讨论：当x≥1时，去绝对值得x-1+2x=a，解得x=
，于是得到a≥2；当x＜1时，去绝对值得1-x+2x=a，解得x=a-1，此时0＜a＜2．
| a+1 |
| 3 |
解答：解：∵
+
=
，
∴x+
+x-
+2
=a，
∴|x-1|+2x=a，
当x≥1时，x-1+2x=a，解得x=
，
则
≥1，解得a≥2，
即a≥2时，x=
；
当x＜1时，1-x+2x=a，解得x=a-1，
则a-1＜1，解得a＜2，
即0＜a＜2时，x=a-1．
x+
|
x-
|
| a |
∴x+
| 2x-1 |
| 2x-1 |
| x2-2x+1 |
∴|x-1|+2x=a，
当x≥1时，x-1+2x=a，解得x=
| a+1 |
| 3 |
则
| a+1 |
| 3 |
即a≥2时，x=
| a+1 |
| 3 |
当x＜1时，1-x+2x=a，解得x=a-1，
则a-1＜1，解得a＜2，
即0＜a＜2时，x=a-1．
点评：本题考查了二次根式的化简求值：二次根式的化简求值，一定要先化简再代入求值．二次根式运算的最后，注意结果要化到最简二次根式，二次根式的乘除运算要与加减运算区分，避免互相干扰．
练习册系列答案
名校课堂系列答案
相关题目
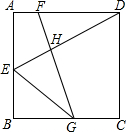如图，在正方形ABCD中，点E是AB上一点，G是BC上一点，FG⊥DE交于点H，FG=DE，求证：FD+EG≥