题目内容
5.已知△ABC的两边AB,AC的长关于x的一元二次方程x2-(2k+3)x+k2+3k+2=0的两个实数根,第三边BC的长为4,若△ABC是等腰三角形,则k=3或4,△ABC的周长为14或16.分析 根据等腰三角形的性质,分三种情况讨论:①AB=AC,②AB=BC,③BC=AC;后两种情况相同,由根与系数的关系得出k的值即可.
解答 解:∵△ABC是等腰三角形,
∴当AB=AC时,△=b2-4ac=0,
∴(2k+3)2-4(k2+3k+2)=0,
解得k不存在;
当AB=BC时,即AB=5,
∴5+AC=2k+3,5AC=k2+3k+2,
解得k=3或4,
∴AC=4或6;
当BC=AC时,即AC=5,同理求得AB=4或6;
∴△ABC的周长为14或16.
故答案为:3或4,14或16.
点评 本题考查了一元二次方程的解法,直角三角形的判定,等腰三角形的性质,根的判别式,根与系数的关系,利用分类讨论是解题的关键.

练习册系列答案
相关题目
16.已知点A的坐标为(2,3),O为坐标原点,连接OA,将线段OA绕点A按顺时针方向旋转90°得AB,则点B的坐标为( )
| A. | (5,1) | B. | (-3,2) | C. | (-1,5) | D. | (3,-2) |
20.下列图形中,内角和与外角和相等的是( )
| A. |  | B. |  | C. |  | D. |  |
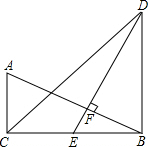 如图,在△ABC和△DBC中,∠ACB=∠DBC=90°,E是BC的中点,DE⊥AB,垂足为点F,且AB=DE.
如图,在△ABC和△DBC中,∠ACB=∠DBC=90°,E是BC的中点,DE⊥AB,垂足为点F,且AB=DE. 在数学课上,老师提出如下问题:
在数学课上,老师提出如下问题: