题目内容
13.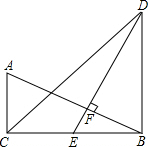 如图,在△ABC和△DBC中,∠ACB=∠DBC=90°,E是BC的中点,DE⊥AB,垂足为点F,且AB=DE.
如图,在△ABC和△DBC中,∠ACB=∠DBC=90°,E是BC的中点,DE⊥AB,垂足为点F,且AB=DE.(1)求证:BD=BC;
(2)若BD=6,则△CDE的面积为9.
分析 (1)欲证明BD=BC,只要证明△ABC≌△EDB即可.
(2)由E是BC中点,BD=6,BD=BC,推出CE=$\frac{1}{2}$BC=$\frac{1}{2}$BD=3,再根据△CDE的面积=$\frac{1}{2}$CE•BD,代入数值计算即可.
解答 (1)证明:∵DE⊥AB,
∴∠BFE=90°,
∴∠ABC+∠DEB=90°,
∵∠ACB=90°,
∴∠ABC+∠A=90°,
∴∠A=∠DEB.
在△ABC和△EDB中,
$\left\{\begin{array}{l}{∠ACB=∠EBD}\\{∠A=∠DEB}\\{AB=ED}\end{array}\right.$,
∴△ABC≌△EDB,
∴BD=BC;
(2)解:∵E是BC中点,BD=6,BD=BC,
∴CE=$\frac{1}{2}$BC=$\frac{1}{2}$BD=3,
∴△CDE的面积=$\frac{1}{2}$CE•BD=$\frac{1}{2}$×3×6=9.
故答案为9.
点评 本题考查了全等三角形的判定和性质,三角形的面积,解题的关键是正确寻找全等三角形,利用全等三角形的性质解决问题,属于中考常考题型.

练习册系列答案
相关题目
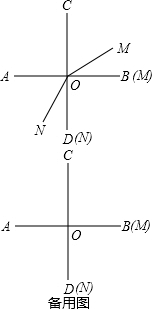 如图,两条直线AB、CD相交于点O,且∠AOC=∠AOD,射线OM(与射线OB重合)绕O点逆时针方向旋转,速度为15°/s,射线ON(与射线OD重合)绕O点顺时针方向旋转,速度为12°/s.两射线OM、ON同时运动,运动时间为t秒.(本题出现的角均指小于平角的角)
如图,两条直线AB、CD相交于点O,且∠AOC=∠AOD,射线OM(与射线OB重合)绕O点逆时针方向旋转,速度为15°/s,射线ON(与射线OD重合)绕O点顺时针方向旋转,速度为12°/s.两射线OM、ON同时运动,运动时间为t秒.(本题出现的角均指小于平角的角) 如图,在等腰直角△ABC中,∠ACB=90°,O是斜边AB的中点,点D、E分别在AC、BC上,且∠DOE=90°,DE交DC于点P,则下列结论:①图中全等的三角形只有两对;②△ABC的面积等于四边形CDOE的面积的2倍;③CD+CE=$\sqrt{2}$OA;④AD2+BE2=2OP•OC.其中正确的结论有( )
如图,在等腰直角△ABC中,∠ACB=90°,O是斜边AB的中点,点D、E分别在AC、BC上,且∠DOE=90°,DE交DC于点P,则下列结论:①图中全等的三角形只有两对;②△ABC的面积等于四边形CDOE的面积的2倍;③CD+CE=$\sqrt{2}$OA;④AD2+BE2=2OP•OC.其中正确的结论有( )